-
Notifications
You must be signed in to change notification settings - Fork 204
Random Forest in R with Large Sample Sizes
Author: Jacob Nearing
First Created: 17 April 2019
Last Edited: 17 April 2019
- Introduction
- Background
- General Workflow
- Running the pipeline yourself
- Random Forest Regression Pipeline
This tutorial is aimed at individuals with a basic background in the R programming language that want to test out how well they can use microbiome sequencing data to either classify samples between different categories or predict a continuous variables outcome. In this tutorial we will go through how to set up your data to be used in training a RF model, as well as the basically principles that surround model training. By the end you will have learned how to create random forest models in R, assess how well they perform and identify the features of importance. Note that this tutorial is generally aimed at larger studies (greater than 100 samples). If you would like to see a similar tutorial on using random Forest with lower sample sizes please see this tutorial.
To Run through this tutorial you will need to have the following packages installed
- Tutorial [ASV Table](link here)
- R (v3.3.2)
- RStudio - recommended, but not necessary (v1.0.136)
- randomForest R package (v4.6-12)
- caret R package (v6.0-73)
- pROC R package
- doMC R package
- DMwR R package
- RandomForest Utility Scripts in this Repo
If you would like to install and load all of the listed R packages manually you can run the following command within your R session:
deps = c("randomForest", "pROC", "caret", "DMwR", "doMC")
for (dep in deps){
if (dep %in% installed.packages()[,"Package"] == FALSE){
install.packages(as.character(dep), repos = "http://cran.us.r-project.org")
}
library(dep, character.only = TRUE)
}
However, the RandomForest Utility Script that is contained within this Repo will automatically install any missing packages and load them into your R session.
Random Forest modelling is one of the many different algorithms developed within the machine learning field. For a brief description of other models that exist check out this [link](link here). Due to this random forest may not always be the optimal machine learning algorithm for your data, however, random forest has been [shown](link here) to perform fairly well on microbial DNA sequencing data, is fairly easy to interrupt and is a great place to start your machine learning adventure.
Random forest models are based off of decision trees a method for classifying categorical and regressing continuous variables within a data set.Decision trees work by helping you to choose which fork in the road is best to go down to get to the optimal result. Imagine your driving down a complex road network and there is two final destinations that you can end up in depending on the turns that you choose to make. Luckily you have lots of information on similar complex road networks others have driven down so you can use the information on what turns they made and where they ended up in the end to determine which turns you should make (this can be thought of as the training dataset more on this later). Well if you have this information you can then use that to make educational guesses to determine which split in the road to take at each turn giving you the best chance at ending up at your desired destination. This is similar to how a decision tree works.
Random forest takes this algorithm further by creating multiple decision trees from different subsets of the training data that you present the algorithm. Each tree that is made then gets to have a vote on which class an object belongs to. For instance if we were to head into a complex road network and give our random forest algorithm all of the various turns we planned to make, each decision tree in the model can then vote on which destination it thinks we would end up in. Generally for classification the final result is whatever class the majority of trees vote on (more on this later).
Random forest models provide multiple advantages compared to single decision trees. They tend to be less over fit to the dataset that they are trained on (although over fitting can still be an issue). They also allow us to evaluate the model by taking subsets of data that trees within the model have never seen before and testing how well those trees perform. This is how we determine the the out-of-bag error rate a useful metric to evaluate how well your model works on predicting the information that it was trained on.
Random forest models also allow users to determine which features within their dataset (in this case microbes) are the most important to make accurate predictions. The importance of each feature within the dataset is determined by scrambling each feature one at a time and re-running the model to determine the change in accuracy. This is useful when trying to determine which microbes may be a major contributing signal between two different classes (such as those with and without disease).
The next section will go over the general work flow of our random forest pipeline and will present what each function within the RF_utlity.R script is doing.accuract
The general workflow falls into three different steps outlined below
Step 1: Splitting Data into training and test datasets This step is a critical step to evaluate model performance and to avoid reporting the performance of models that are grossly over fit. The idea here is quite simple you take your dataset and split them up into training data and testing data. This split then allows you to determine how well your model would perform on data that it has never seen before which is important to evaluate whether or not your model is over fit. Generally this split is done so that the majority of data is kept for training and a small subset is used for testing purposes. In this tutorial we will use 20% of the data for testing and 80% for training.
Step 2: Model Training Once you have your training dataset the next step is begin training your model. There are two parameters that can be changed in this step for random forest modelling; the number of trees and the number of splits at each node in the trees (mtry).
In general as the number of trees increase the performance of the model will increase until a plateau is reached. This plateau can vary between data sets and sometimes its worth trying multiple numbers to find the optimal number of trees. You can always set a very large number for this value and not worry about this issue, however, this will sever## Our Pipeline We will begin this section by going over the functions of the random forest classification pipeline. This will help you understand how each function works and how to interrupt the data that results from them. ely impact the run time.
Determine the best mtry is a bit more difficult because it varies from dataset to dataset. A good starting point is usually the square root of the number of features.
mTry is known as a hyper-parameter and tuning hyper-parameters in appropriately can lead to model over fitting, which leads us to cross-validation. Cross-validation is one of many different methods that can be used to combat over fitting when tuning hyper parameters. In this case we will focus of k-fold repeated cross validation. K-fold cross validation works by taking the training dataset supplied to the model algorithm and further splitting them up into k even numbered data sets. A model is then trained on each dataset and validated on the other data sets. This helps further protect against picking hyper-parameters that just happen to work really well on the split you made between training and test. Generally this process is then repeated n times to determine which mtry value works best overall allowing you to pick a final "best" model.
Step 3 Model Validation This final step is where the test dataset comes into play. During this step you will take the final model from training and use it to make classifications (for categorical variables) or regressions (for continuous variables) on the hold out test set. This will allow you to determine how well you can expect your model to work on data that it has never come across. This is important when reporting things such as how well your model can predict disease outcome.
This section will go through how to run the random forest pipeline on a dataset that can be found [here]. This dataset was published in [2015 by Singh et al.,](link to paper) who were interested in looking a differences between healthy individuals and those with enteric infections.
The first step will be to read in the dataset and cleaning up the data
Set your working directory
setwd("/Path/to/my/RF_tutorial/")
Read in the count table of genera and the metadata associated to each sample
Genus_values <- read.table("edd_singh_genera.tsv",
sep="\t", header=T, row.names=1)
metadata <- read.table("edd_singh.metadata.clean.tsv",
sep="\t", header=T, row.names=1)
Lets inspect these tables a bit
dim(Genus_values)
[1] 153 283
We can see that the genus table has 283 different columns and 158 rows. Each column represents a different sample and each row represents a different genus. We will next want to clean up these two tables so that they only include samples that had greater than 1000 reads
indexs_to_keep <- which(metadata$total_reads >= 1000)
length(indexs_to_keep)
[1] 272
In total we have 272 samples that have more than 1000 reads. We will use this list of indexes to subset our original table.
clean_Genus_values <- Genus_values[,indexs_to_keep]
clean_metadata <- metadata[indexs_to_keep,]
dim(clean_Genus_values)
[1] 153 272
dim(clean_metadata)
[1] 272 10
rownames(clean_metadata) <- gsub("-","\\.",rownames(clean_metadata))
all.equal(colnames(clean_Genus_values), rownames(clean_metadata))
[1] TRUE
Great the dimensions still match up and so do the row names. Now that this is complete the next step we will want to take is to remove genera that are "rare" meaning those that are only found in a small amount of the total samples. To do this we will need to run the follow lines of code to load in our remove rare feature function:
remove_rare <- function( table , cutoff_pro ) {
row2keep <- c()
cutoff <- ceiling( cutoff_pro * ncol(table) )
for ( i in 1:nrow(table) ) {
row_nonzero <- length( which( table[ i , ] > 0 ) )
if ( row_nonzero > cutoff ) {
row2keep <- c( row2keep , i)
}
}
return( table [ row2keep , , drop=F ])
}
This function will remove any rows (genera) that are non-zero in less than some cutoff proportion of samples. For this dataset we set the cutoff proportion to 20% (0.2) (so we will discard Genera that are 0 in 80% or more of the samples).
non_rare_genera <- remove_rare(clean_Genus_values, 0.2)
dim(non_rare_genera)
[1] 58 272
Removal of rare features using these parameters left us with 58 of the original 153 genera. The next step in our data pre-processing will be to convert our count data into a different representation. Common pre-processing procedures will convert data into Relative abundance, center-log ratio or even PCA variables (given enough features). In this case we have chosen to convert our count table into center-log-ratio values with a pseudo-count of 1. A pseudo count of 1 is required as the value of log(0) is undefined!
input_features <- data.frame(apply(non_rare_genera +1, 2, function(x) {log(x) - mean(log(x))}))
colSums(input_features)
You will notice that all of the colSums add up to very small close to zero 0 numbers a good indication that our above function worked correctly. The RF pipeline from our script expects that samples are rows and microbes are columns so we need need to flip our input_features table.
input_features <- data.frame(t(input_features))
Finally the last step is to set-up the classes of each sample that we want to predict.
classes <- factor(ifelse(clean_metadata$DiseaseState=="EDD","Case","Control"), levels=c("Case","Control"))
In this case EDD will represent Case samples of enteric infections and H will represent Control samples.
We now have all the features ready to input into our model as well as the classes those features represent. To run our model we can use the run_rf_classifcation_pipeline() function found in the RF_utilities.R script in this repository. We can run the script with the following commands:
Set the seeds so that our results are can be reproduced:
set.seed(1995)
seeds <- sample.int(1000000, 10)
Next we can call the main RandomForest Pipeline: To get an explaination of each parameter for this function run the following:
get_rf_results(help=T)
Example of function usage: get_rf_results(feature_table = input_features, classes = classes, metric='ROC')
Explanation of each parameter:
feature_table: The input feature table that you want to use to predict the input to classes. The format of
this table should be that rows equal samples and columns equal features (such as abundance of each microbe).
classes: The classes of each sample that is found in the rows of the feature table. Make sure that the
classes order matches the sample order in feature_table.
metric: This is the metric that you want to evaluate your model with. The default for this is 'ROC' which
will evaluate model performance based on AUC of a ROC curve. Other available options are 'PR' which
evaluates based on the AUC of a precision recall curve, this is useful for unbalanced class designs.
sampling: This is used to set the sampling strategy during model training. The default is NULL meaning no
special sampling will be done and should be used in balance class designs. Options include up-
sampling, down-sampling, and smote-sampling.
repeats: the number of training and test data splits you want to be done. Default: 10
path: this is the path that you want to save the results of this pipeline to.
nmtry: is the number of mtry parameters you want to test during model optimisation. Default: 3
ntree: the number of trees you want you model to use. Default: 1001
nfolds: the number of even folds to split your data into during cross validation. Default: 3
ncrossrepeats: the number of times you want to repeat cross validation for each data split. Default: 10
pro: The proportion of data that is used as training data. The other proportion will be used as a test
/validation dataset. Default: 0.8
list_of_seeds: A list of random seeds that must be equal to or longer than the number input into repeats.
help: Set to TRUE in order to see these messages!
version: set to TRUE to print out the version of this pipeline
values: set to TRUE to print out the expected results from this function
In general most of this parameters won't need much changing for most models. For robust estimates in accuracy you may want to increase the number of repeats to 100+, however starting at 10 to get a baseline estimate of accuracy is acceptable.
SAVE_PATH <- "path/to/save/rf/results/"
rf_results <- get_rf_results(feature_table = input_features, classes = classes, metric="ROC", sampling=NULL,
repeats=10, path=SAVE_PATH, nmtry=4, ntree=1001, nfolds=3,
nvalues: set to TRUE to print out the expected results from this functioncrossrepeats = 5, pro = 0.8, list_of_seeds = seeds)
To get an idea of what this function returns we can run the following command:
get_rf_results(values=T)
This function returns an object with the follow characteristics:
Object[[1]] contains all the median cross validation AUCS from each data split using the best mtry value
Object[[2]] contains all the test AUC values from each data split
Object[[3]] contains all the tested mtry values and the median ROC for each from each data split
Object[[4]] contains the list of important features from the best model selected from each data split
Object[[5]] contains each caret random forest model from each data split
This function will also write a csv with cv AUCS and test AUCS, to the given path as well as an RDS file
that contains the resulting object from this function.
Now that we know what our function is doing lets look at the results. First we will compare cross validation AUCS with test AUCS to get an idea if our model is over fit or not.
boxplot(rf_results[[1]], rf_results[[2]], names=c("Cross Validation AUC", "Test AUC"))
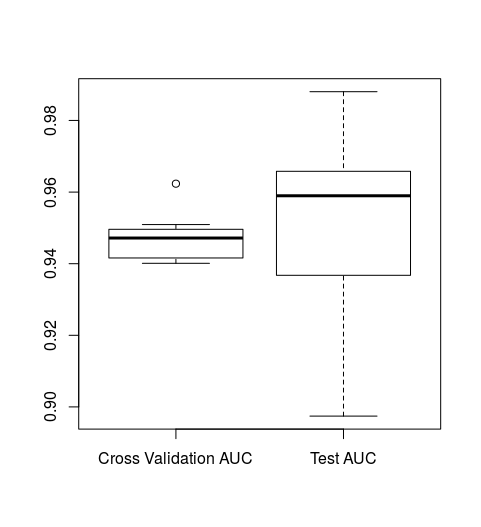
We can see that our test/validation AUCs and cross validation AUCS are similar indicating that our model doesn't seem to over fit. We also see that our model's ROC AUC on data that it has never seen before (the test dataset) is rough ~0.95. We can confirm this by running the following:
mean(rf_results[[2]])
[1] 0.9505983
This is an extremely good ROC AUC, which indicates that our model is most likely significantly better than random classification. To confirm this we can run a second pipeline that will scramble our class data and run the same random forest pipeline. We can then compare AUCS to determine whether or not or model is significantly better than random.
First we need to generate lists of scrambled data:
scrambled_classes <- list()
set.seed(1880)
for(i in 1:10){
scrambled_classes[[i]] <- sample(classes)
}
We can then pass these new scrambled class lists into the get_random_rf_results(). This function takes in the exact same inputs as the get_rf_results() function except that the classes parameter is replaced by the list of scrambled classes that we just made. Not that we suggest in practice to increase the number of scrambled classes and repeats to 100+. But for time reasons we will stick to 10 for this tutorial.
rf_random_results <- get_random_rf_results(feature_table = input_features, list_of_scrambles =
scrambled_classes, metric="ROC", sampling=NULL,
repeats=10, path=SAVE_PATH, nmtry=4, ntree=1001, nfolds=3,
ncrossrepeats = 5, pro = 0.8, list_of_seeds = seeds)
We can now compare our cross validation ROC AUCs between our real classes and when the classes are randomised.
boxplot(rf_results1, rf_random_results1, names=c("Cross Validation ROC AUC Real", "Cross Validation
ROC AUC Random"))
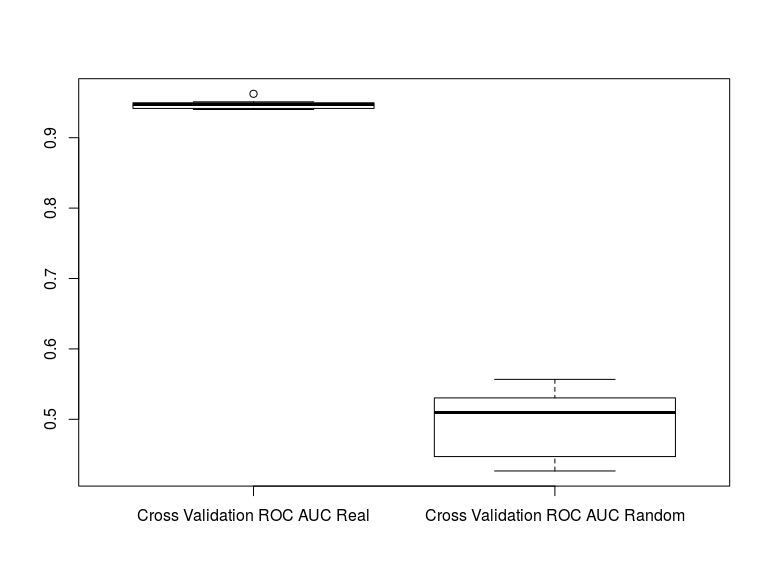
We can see that are model is much better than random and can further test for significance with:
t.test(rf_results[[1]], rf_random_results[[1]])
Welch Two Sample t-test
data: rf_results[[1]] and rf_random_results[[1]]
t = 29.496, df = 9.3248, p-value = 1.59e-10
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.4154063 0.4840234
sample estimates:
mean of x mean of y
0.9474799 0.4977651
This tells us that our model has a significantly better cross validation AUC when compared to random permutations of the class labels.
We can also check to see how our test AUCs match up.
boxplot(rf_results2, rf_random_results2, names=c("Test ROC AUC Real", "Test ROC AUC Random"))
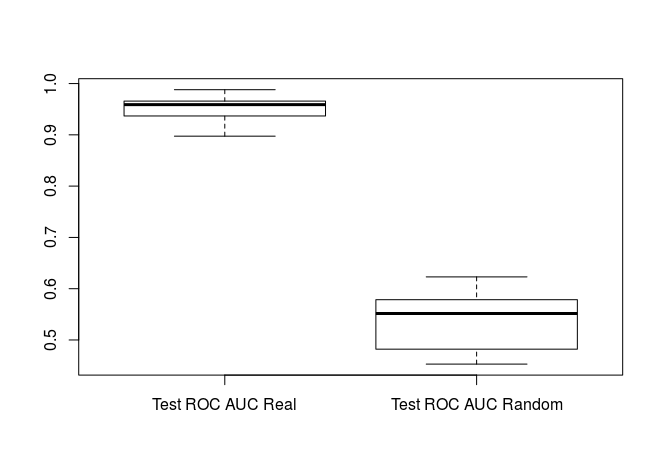
t.test(rf_results[[2]], rf_random_results[[2]])
Welch Two Sample t-test
data: rf_results[[2]] and rf_random_results[[2]]
t = 20.593, df = 12.649, p-value = 4.164e-11
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.3674023 0.4537942
sample estimates:
mean of x mean of y
0.9505983 0.5400000
Again we see that our test/validation ROC AUCs are significantly better than random indicating that our model is significantly better than random classification.
One thing that we may be interested in when examining our data is what features are the best predictors of classification. This can be done by taking advantage of the important features data frames returned to us for each data split that we performed. We can inspect the top features from the first data split we did by running the following commands:
split1_impt_feats <- as.data.frame(rf_results[[4]][[1]])
split1_impt_feats <- split1_impt_feats[order(split1_impt_feats$t1MeanDecreaseAccuracy, decreasing=T),]
split1_impt_feats[1:1, ]
t1Case t1Control t1MeanDecreaseAccuracy t1MeanDecreaseGini
....f__Ruminococcaceae._.g__Clostridium_IV 0.009192336 0.09732973 0.0328612 12.87789
From this we can see that the top feature for data split 1 was Clostridium_IV and when this feature is randomly permuted within the data set it results in a decrease in accuracy of roughly 3.3%. But what about the other data splits???
Well what we can do is combined all the the feature information from each data split and then take the mean value of the decrease in accuracy to determine which features were the most important in all data splits. This helps to avoid identifying features that are only important in one data split due to the way the data was divided. This is fairly simple to do running the following code:
Total_impt_feats_decrease_in_accuracy <- Calc_mean_accuray_decrease(rf_results[[4]])
Total_impt_feats_decrease_in_accuracy[1:1, c("Mean", "SD", "Min", "Max")]
Mean SD Min Max
......g__Cronobacter 0.02586557 0.004608841 0.01543898 0.03131443
This tells us that the most important feature overall from all of the data splits is actually Cronobacter! If we examine the table a bit more we will notice that Clostridium_IV is actually the third most important
Total_impt_feats_decrease_in_accuarcy[1:3, c("Mean", "SD", "Min","Max")]
Mean SD Min Max
....g__Cronobacter 0.02586557 0.004608841 0.01543898 0.03131443 .....f__Enterobacteriaceae._.g__ 0.02123790 0.006075840 0.01235502 0.03257328 .....g__Clostridium_IV 0.02118547 0.007857878 0.01254713 0.03643650
As we can see they are all fairly close so there wasn't one feature that was a silver bullet in this case. This is the end to the classification tutorial the next section will go over using microbiome data to predict a continuous metadata using regression.
- Please feel free to post a question on the Microbiome Helper google group if you have any issues.
- General comments or inquires about Microbiome Helper can be sent to [email protected].