forked from YaccConstructor/QuickGraph
-
-
Notifications
You must be signed in to change notification settings - Fork 71
Traversal Concepts
Alexandre Rabérin edited this page May 12, 2020
·
1 revision
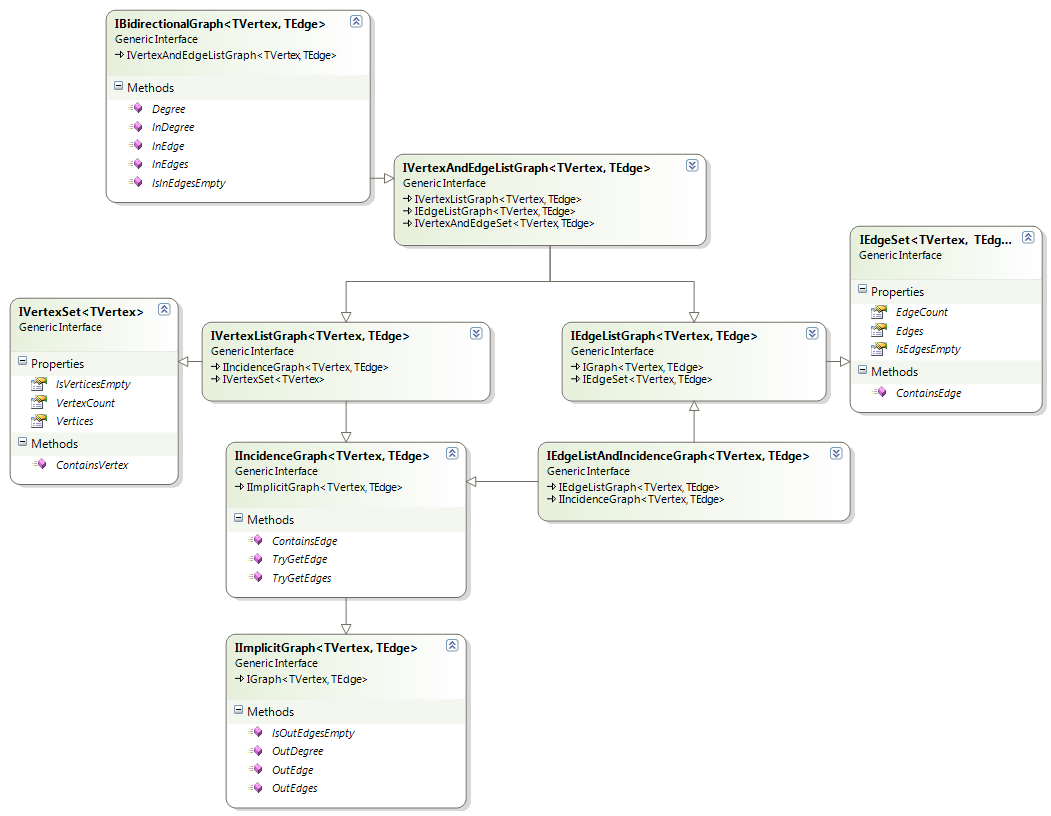
The traversal concepts define the different ways the vertices and edges of a graph can be accessed and enumerated.
Tip:
All the interfaces depend on 2 generic parameters
TVertexandTEdge, whereTEdgehas the additional constraint of implementingIEdge<TVertex>.
Each of these interfaces is described below (generic arguments have been omitted for the sake of clarity):
-
IImplicitGraphdefines a graph that contains information about the out-edges of a vertex. This interface is particularly important when the size of your graph is infinite and you only have “local information”. -
IIncidenceGraphextends IImplicitGraph by providing the out-edges count. -
IVertexListGraphdefines a graph that publishes the collection of vertices. With this concept, one can iterate the vertices and access the out-edges of each vertex. This is an important concept that is used by many algorithms. -
IEdgeListGraphdefines a graph that publishes the collection of edges. No information about out-edges is available. -
IVertexAndEdgeListGraphmerges IVertexListGraph and IEdgeListGraph functionalities -
IBidirectionalGraphdefines a vertex list graph that also publishes the in-edges. Such graph can be used to explore a graph in a both directions.