Depth First Search Example

Depth First Search Example

Let us illustrate how algorithms work by applying a depth-first-search algorithm on a simple graph.

When possible, a depth-first traversal chooses a vertex adjacent to the current vertex to visit next. If all adjacent vertices have already been discovered, or there is no adjacent vertex, then the algorithm backtracks to the last vertex that had undiscovered neighbors. Once all reachable vertices have been visited, the algorithm selects from any remaining undiscovered vertices and continues the traversal. The algorithm finishes when all vertices have been visited. Depth-first search is useful for categorizing edges in a graph, and for imposing an ordering on the vertices.

The depth-first-search algorithm is part of a family of graph algorithms that colorize vertices. By convention such algorithms always use the same 3 color markers:

• White: vertex not yet discovered
• Gray: vertex discovered, and sub-tree being explored
• Black: vertex discovered and sub-tree traversal finished

Tip:

In QuikGraph, algorithms that colorize vertices implement the IVertexColorizerAlgorithm interface.

The depth first search is implemented by the DepthFirstSearchAlgorithm class. This class exposes a number of events (not all are detailed here) that are used by observers:

• InitializeVertex invoked on each vertex before starting the computation.
• DiscoverVertex invoked when a vertex is encountered for the first time.
• ExamineEdge invoked on every out-edge of each vertex after it is discovered.
• TreeEdge invoked on each edge as it becomes a member of the edges that form the search tree.
• FinishVertex invoked on a vertex after all of its out-edges have been added to the search tree and all of the adjacent vertices have been discovered (but before their out-edges have been examined).

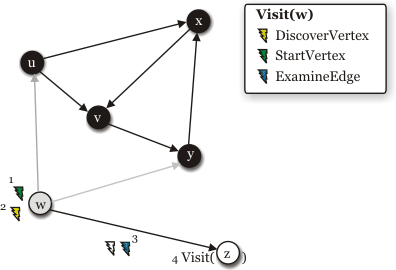
The application of the depth first search to a simple graph is detailed in the figures below. The code to achieve this looks (more or less) as follows:

// A graph that implements the IVertexListGraph interface
var graph = new AdjacencyGraph<TVertex, TEdge>();
...
// Create algorithm
var dfs = new DepthFirstSearchAlgorithm<TVertex, TEdge>(graph);
// Do the search
dfs.Compute();

• InitializeVertex event is triggered on each vertex.

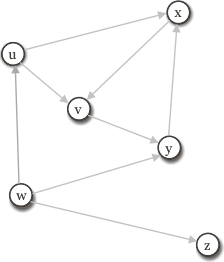
• Visiting u vertex yields to the following event triggers:
  • StartVertex(u),
  • DiscoverVertex(v),
  • ExamineEdge(u,v),
  • TreeEdge(u,v)

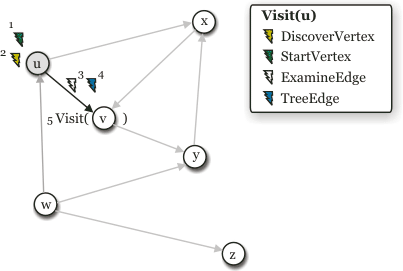
• Visiting v vertex,

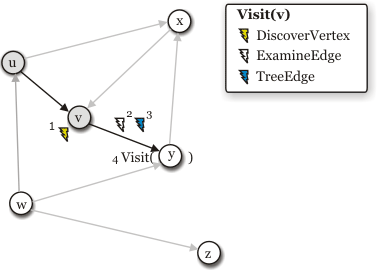
• Visiting y vertex,

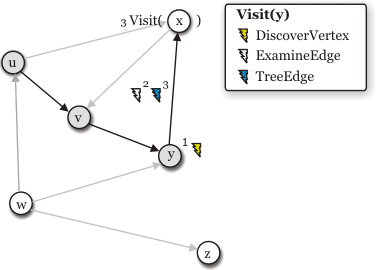
• Visiting x vertex. The edge (x,v) is a back edge, i.e. it points to a gray vertex. Since there are no more out-edges to explorer, the vertex is finished and blacked.

• Finishing u vertex. The edge (u,x) is a cross-edge because it points to a black vertex (x).

• Since w was not reachable from u, the search is restarted.

Tip :

The algorithm will not reach w and z if you set a root vertex with dfs.SetRootVertex(rootVertex), but you can request to process all vertices by setting dfs.ProcessAllComponents to true.

• Finishing graph

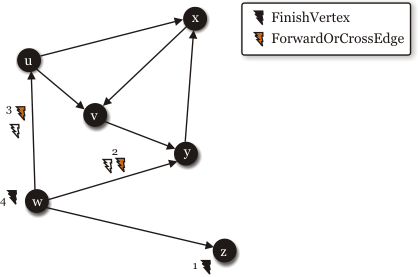
The figures above show when the events are called. The events are used by the observers to record data. For example, using the TreeEdge event one can extract a tree out of the graph. The tree is recorded under the form of a dictionary associating each vertex with it’s predecessor.

Dictionary<TVertex, TEdge> verticesPredecessors;
void TreeEdgeHandler(object sender, TEdge edge)
{
    VerticesPredecessors[edge.Target] = edge;
}

dfs.TreeEdge += new EdgeEventArgs<TVertex, TEdge>(TreeEdgeHandler);

In fact, this is what the VertexPredecessorRecorderObserver does by building one a table of vertex parents.

var dfs = new DepthFirstSearchAlgorithm<TVertex, TEdge>(graph);
var observer = new VertexPredecessorRecorderObserver<TVertex, TEdge>();
using (observer.Attach(dfs)) // Attach/detach to DFS events
{
    dfs.Compute();
}

// observer.VerticesPredecessors is a IDictionary<TVertex, TEdge> that links vertices to their parent edges

Filtered Depth First Search Example

When going through all the tree is undesired, QuikGraph allows to use outEdgesFilter function to avoid going in undesirable areas of the graph. The following example shows how to filter edges of a currently visited vertex.

var graph = new AdjacencyGraph<TVertex, Edge<TVertex>>();

// Setup your graph the way you want

IEnumerable<Edge<TVertex>> Filter(IEnumerable<Edge<TVertex>> edges)
{
    // Your filtering algorithm here
    // Ex: edges.Where(e => ...)
    // Or
    // if (...)
    // {
    //     yield ...;
    // }
}

// Create algorithm
var dfs = new DepthFirstSearchAlgorithm<TVertex, Edge<TVertex>>(
    null,
    graph,
    new Dictionary<TVertex, GraphColor>(),
    Filter);    // <=
// Do the search
dfs.Compute();