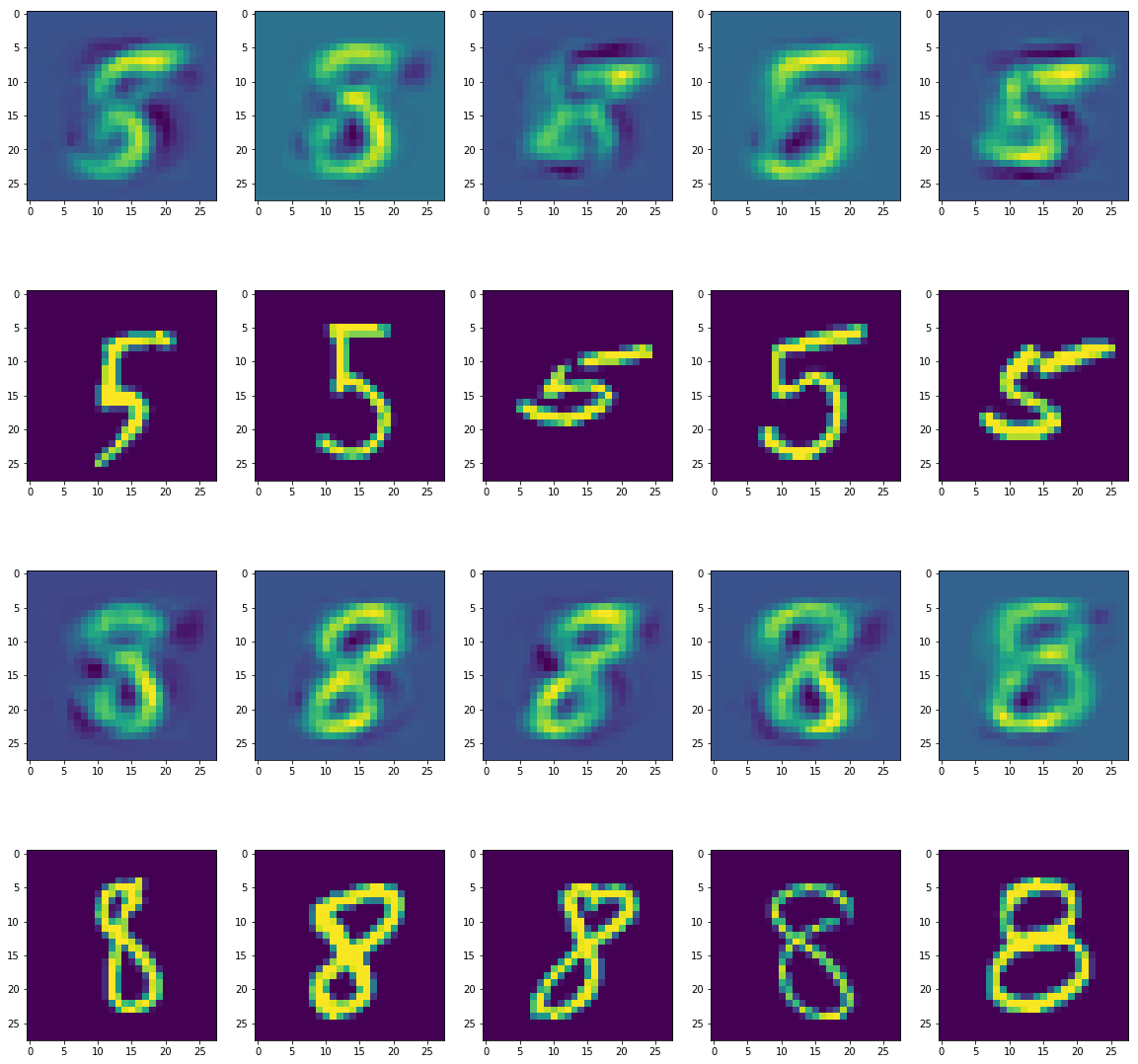Pricipal Component Analysis (PCA) also known as Karhunen-Loeve transform, is widely used for the purpose of dimensionallity reduction, feature extraction, and data visualization. It provides a way for lossy data compression, orthogonally projecting the data onto a lower dimensional space. The goal is to reduce the dimensionality from D dimensions, here 784 (28X28 image flattened), to a lower dimension M such that the variance of the projected data is maximized.
Let x represent one data points out of N examples, and mu is the mean of N data samples then the PCA will include calculating the covariance matrix S, M largest eigen values of S and the corresponding M eigen vectors represented by A:
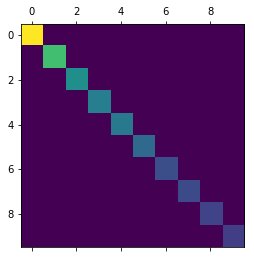
After PCA for reducing the dimension from 784 to 10, the covariance of the data points looks like following:
On PCA whitening, or on calculating , we can see the lossy compression of the images:
Reduced to two dimensions using PCA
Result of Fisher's LDA analysis:
| Metric Description | Result |
|---|---|
| training accuracy | 93.0% |
| Class 0 (true label = 5) training accuracy | 95.5% |
| Class 1 (true label = 8) training accuracy | 90.5% |
| test accuracy | 71% |
| Class 0 (true label = 5) test accuracy | 6.0% |
| Class 1 (true label = 8) test accuracy | 94.0% |