Transformers

A pytorch implementation of transformers.

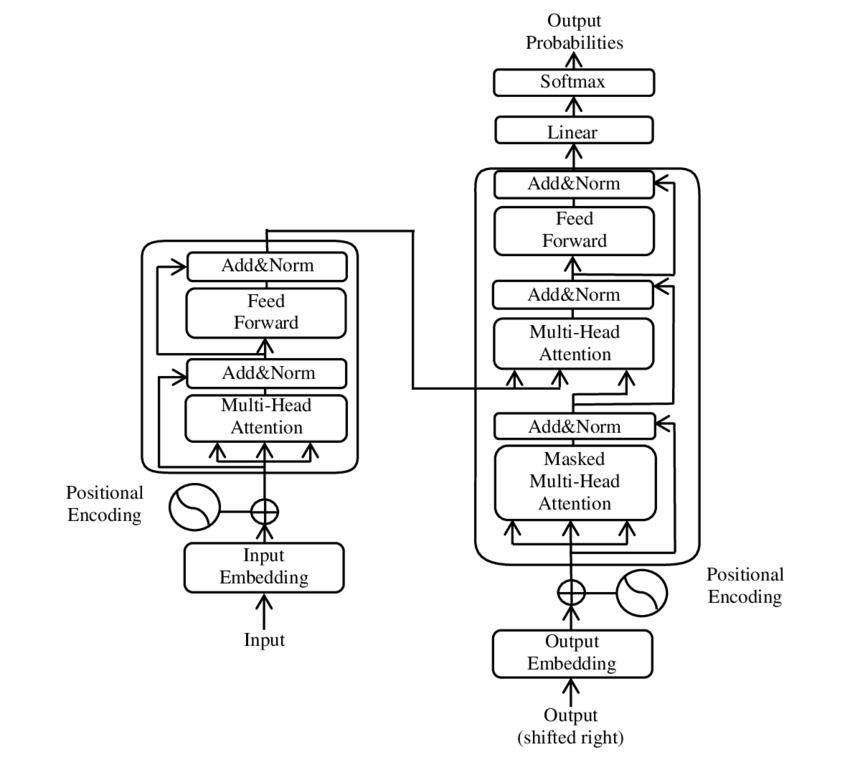
This repository contains the implementation of the transformer model as described in the paper "Attention is All You Need" (2017). The implementation is based on the original paper and it's written in PyTorch with learning purposes only, since PyTorch already provides optimized implementations of the transformer model that you can import as:

from torch.nn.functional import scaled_dot_product_attention
from torch.nn import MultiheadAttention
from torch.nn import TransformerEncoderLayer
from torch.nn import TransformerDecoderLayer
from torch.nn import Transformer

The paper introduces the following concepts:

Positional Encoding

Let $X \in \mathbb{R}^{l \times d}$ a sequence of $l$ vectors embeddings of dimension $d$.

$$X = \begin{bmatrix} \vec{x}^1 \\ \vec{x}^2 \\ \vdots \\ \vec{x}^l \end{bmatrix} = \begin{bmatrix} x^1_1 & x^1_2 & \cdots & x^1_d \\ x^2_1 & x^2_2 & \cdots & x^2_d \\ \vdots & \vdots & \ddots & \vdots \\ x^l_1 & x^l_2 & \cdots & x^l_d \end{bmatrix} $$

With $\vec{x}^t \in \mathbb{R}^d$ the embedding vector of the word at position $t$ in the sequence. To inform the embedding vectors about their position, each one is added the vector $\vec{p} ^ t$ that we will describe below.

$$\vec{p}^t = \begin{bmatrix} p^t_1 & p^t_2 & \cdots p^t_d \end{bmatrix}$$

The attention is all you need paper, proposes a positional encoding function $\text{P}:\mathbb{N}\times\mathbb{N}\rightarrow\mathbb{R}^d$ as:

$$\text{P}(t, s) = \begin{cases} \sin(\omega_k t) & \text{si } s = 2k \\ \cos(\omega_k t) & \text{si } s = 2k + 1 \end{cases}$$

With the "frequencies" defined by $$\omega_k = \frac{1}{N ^ {2 k /d}} = \exp(-\frac{2k}{d}\log(N))$$

And a constant $N$.

The positional encoding matrix $P \in \mathbb{R}^{l \times d}$ will be:

$$ P = \begin{bmatrix} 0 & 1 & 0 & 1 & \cdots & 0 & 1 \\ \sin(\omega_1) & \cos(\omega_1) & \sin(\omega_2) & \cos(\omega_2) & \cdots & \sin(\omega_{d/2}) & \cos(\omega_{d/2}) \\ \sin(\omega_1 2) & \cos(\omega_1 2) & \sin(\omega_2 2) & \cos(\omega_2 2) & \cdots & \sin(\omega_{d/2} 2) & \cos(\omega_{d/2} 2) \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ \sin(\omega_1 (l-1)) & \cos(\omega_1 (l-1)) & \sin(\omega_2 (l-1)) & \cos(\omega_2 (l-1)) & \cdots & \sin(\omega_{d/2} (l-1)) & \cos(\omega_{d/2} (l-1)) \end{bmatrix} $$

The positional encoding matrix $P$ is pre-computed only once and is added to the sequence of embeddings $X$ at each step of the network.

$$X := X + P$$

class PositionalEncoding(Module):
    def __init__(self, sequence_lenght_limit: int, model_dimension: int, scaling_factor: int = 10000, device=None, dtype=None):
        super().__init__()
        self.embeddings = Parameter(data=torch.zeros(sequence_lenght_limit, model_dimension, device=device, dtype=dtype), requires_grad=False)
        for dimension in range(model_dimension):
            self.embeddings[:,dimension] = dimension // 2 + 1
            self.embeddings[:,dimension] = exp(-2*self.embeddings[:,dimension] * math.log(scaling_factor) / model_dimension)
            for sequence in range(sequence_lenght_limit):
                if dimension % 2 == 0:
                    self.embeddings[sequence,dimension] = sin(sequence * self.embeddings[sequence,dimension])
                else:
                    self.embeddings[sequence,dimension] = cos(sequence * self.embeddings[sequence,dimension])

    def forward(self, input: Tensor) -> Tensor:
        input = input + self.embeddings[:,:input.size(1)]
        return input

Self-Attention

Given three tensors $Q, K, V \in \mathbb{R}^{l \times d_k}$, $\mathbb{R}^{l \times d_k}$ and $\mathbb{R}^{l \times d_v}$ respectively, the attention is calculated as:

$$ \text{Attention}(Q, K, V) = \text{Softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V $$

def attention(query: Tensor, key: Tensor, value: Tensor, mask: Optional[Tensor] = None) -> Tensor:       
    scale = 1 / math.sqrt(key.size(-1))
    score = query @ key.transpose(-2, -1) * scale
    if mask is not None:
        score = score.masked_fill(mask == 0, float('-inf'))
    return softmax(score, dim=-1) @ value

Multi-Head Attention

In the transformers model, the attention mechanism is applied in parallel to multiple projections of the queries, keys and values. Each projection is called an "attention head". To define these projections, three weight matrices $W^Q$, $W^K$ and $W^V$ are used that are applied to the queries, keys and values respectively.

Let:

• $W^Q \in \mathbb{R}^{d \times d_q}$
• $W^K \in \mathbb{R}^{d \times d_k}$
• $W^V \in \mathbb{R}^{d \times d_v}$

With $d_q = d_k$. Given a tensor $X \in \mathbb{R}^{l \times d}$, we say that the products:

• $X W^Q \in \mathbb{R}^{l \times d_k} $
• $X W^K \in \mathbb{R}^{l \times d_k} $
• $X W^VX \in \mathbb{R}^{l \times d_v} $

Are the projections of the tensor $X$ in the query, key and value spaces respectively. We can then define the multi-head attention mechanism as:

$$ \text{MultiHead}(Q, K, V) = \text{Concat}(\text{head}_1, \text{head}_2, \cdots, \text{head}_h) W^O $$ $$ \text{head}_i = \text{Attention}(Q W^Q_i, K W^K_i, V W^V_i) $$

With $Q W^Q_i$, $K W^K_i$ and $V W^V_i$ the projections of the tensors $Q$, $K$ and $V$ in the query, key and value spaces respectively, for a head $\text{head}_i$, and $W^O$ is another transformation that is applied to the result of concatenating the outputs of each head. These transformations are responsible for generating the different "heads" from the queries, keys and original values.

Although in the definition of the multi-head attention mechanism layer, different views are generated for the input tensors $Q$, $K$ and $V$, in practice, it is simpler and computationally more efficient to generate a single projection of these tensors and then divide them into $h$ parts, so that the matrices $Q_i$, $K_i$ and $V_i$ are generated for each head $i$. This can be achieved as follows:

Given a projection $P \in \mathbb{R}^{l \times d}$, either $P = W^Q Q, W^K K$ or $W^V V$ we can divide each row of $P$ into $h$ parts of dimension $d/h$ and then group the vectors of each part into a matrix of dimension $l \times d/h$ in the same tensor by adding a dimension as follows:

$$ P = \begin{bmatrix} p^1_1 & p^1_2 & \cdots & p^1_d \\ p^2_1 & p^2_2 & \cdots & p^2_d \\ \vdots & \vdots & \ddots & \vdots \\ p^l_1 & p^l_2 & \cdots & p^l_d \\ \end{bmatrix} \rightarrow \begin{bmatrix} \begin{bmatrix} p^1_1 & \cdots & p^1_{d/h} \\ \vdots & \vdots & \ddots & \vdots \\ p^1_{d\frac{(h-1)}{h}+1} & \cdots & p^1_d \\ \end{bmatrix} \\ \vdots \\ \begin{bmatrix} p^l_1 & \cdots & p^l_{d/h} \\ \vdots & \ddots & \vdots \\ p^l_{d\frac{(h-1)}{h}+1} & \cdots & p^l_d \\ \end{bmatrix} \\ \end{bmatrix} \rightarrow \begin{bmatrix} \begin{bmatrix} p^1_1 & p^1_2 & \cdots & p^1_{d/h} \\ \vdots & \vdots & \ddots & \vdots \\ p^l_1 & p^l_2 & \cdots & p^l_{d/h} \\ \end{bmatrix} \\ \vdots \\ \begin{bmatrix} p^1_{d\frac{(h-1)}{h}+1} & \cdots & p^1_d \\ \vdots & \vdots & \vdots \\ p^l_{d\frac{(h-1)}{h}+1} & \cdots & p^l_d \\ \end{bmatrix} \\ \end{bmatrix} $$

Where the first matrix is the first head, the second matrix is the second head and so on. The final result is a tensor of dimension $h \times l \times d/h$.

The concatenation of the outputs of each head is done in the dimension $d/h$ and is the inverse process to the one described for the "split" so that the final result is a tensor of dimension $l \times d_v$.

Finally, the output is multiplied by the matrix $W^O \in \mathbb{R}^{d_v \times d}$ to obtain the final result of the multi-head attention layer, which will have dimension $l \times d$.

Note that $h$ projectors $W^P$ of dimension $d/h \times d_p$ and multiplying them by the input tensors, is equal to defining a single tensor $W^P$ of dimension $d \times d_p$ with which a single projection $P$ is generated, from the input tensor, and then perform the "split" of the dimension $d$ into $h$ parts.

So the multi-head attention mechanism will be:

$$ \text{Attention}(Q, K, V) = \text{Softmax}( \begin{bmatrix} \begin{bmatrix} q^1_1 & q^1_2 & \cdots & q^1_{d_k/h} \\ \vdots & \vdots & \ddots & \vdots \\ q^l_1 & q^l_2 & \cdots & q^l_{d_k/h} \\ \end{bmatrix} \begin{bmatrix} k^1_1 & k^2_1 & \cdots & k^l_1 \\ \vdots & \vdots & \ddots & \vdots \\ k^1_{d_k/h} & k^2_{d_k/h} & \cdots & k^l_{d_k/h} \\ \end{bmatrix} \\ \vdots \\ \begin{bmatrix} q^1_{d_k\frac{(h-1)}{h}+1} & \cdots & q^1_{d_k} \\ \vdots & \vdots & \ddots & \vdots \\ q^l_{d_k\frac{(h-1)}{h}+1} & \cdots & q^l_{d_k} \\ \end{bmatrix} \begin{bmatrix} k^1_{d_k\frac{(h-1)}{h}+1} & \cdots & k^l_{d_k\frac{(h-1)}{h}+1} \\ \vdots & \vdots & \vdots\\ k^1_{d_k} & \cdots & k^l_{d_k} \\ \end{bmatrix} \\ \end{bmatrix} / \sqrt{d_k/h} ) \begin{bmatrix} \begin{bmatrix} v^1_1 & v^1_2 & \cdots & v^1_{d_v/h} \\ \vdots & \vdots & \ddots & \vdots \\ v^l_1 & v^l_2 & \cdots & v^l_{d_v/h} \\ \end{bmatrix} \\ \vdots \\ \begin{bmatrix} v^1_1 & v^1_2 & \cdots & v^1_{d_v/h} \\ \vdots & \vdots & \ddots & \vdots \\ v^l_1 & v^l_2 & \cdots & v^l_{d_v/h} \\ \end{bmatrix} \end{bmatrix} $$

Where each matrix inside the tensors corresponds to an attention head. The result of the attention function is a tensor of dimension $h\times l\times l$. Which is multiplied by the tensor $V$ resulting in a tensor of dimension $h \times l \times d_v/h$.

The concatenation of the outputs of each head is done in the dimension $d_v/h$ and is the inverse process to the one described for the "split" so that the final result is a tensor of dimension $l \times d_v$.

Finally, the output is multiplied by the matrix $W^O \in \mathbb{R}^{d_v \times d}$ to obtain the final result of the multi-head attention layer, which will have dimension $l \times d$.

def split(sequence: Tensor, number_of_heads: int) -> Tensor:
    batch_size, sequence_length, model_dimension = sequence.size()
    sequence = sequence.view(batch_size, sequence_length, number_of_heads, model_dimension // number_of_heads)
    sequence = sequence.transpose(1, 2)
    return sequence

def concat(sequence: Tensor) -> Tensor:
    batch_size, number_of_heads, sequence_lenght, heads_dimension = sequence.size()
    sequence = sequence.transpose(1, 2).contiguous()
    sequence = sequence.view(batch_size, sequence_lenght, heads_dimension* number_of_heads)
    return sequence

class MultiheadAttention(Module):
    def __init__(self, model_dimension: int, key_dimension: int, value_dimension: int, number_of_heads):
        super().__init__()
        self.number_of_heads = number_of_heads
        self.query_projector_weight = Parameter(torch.empty(model_dimension, model_dimension))
        self.key_projector_weight = Parameter(torch.empty(model_dimension, key_dimension))
        self.value_projector_weight = Parameter(torch.empty(model_dimension, value_dimension))
        self.output_projector_weight = Parameter(torch.empty(model_dimension, model_dimension))

        init.xavier_normal_(self.query_projector_weight)
        init.xavier_normal_(self.key_projector_weight)
        init.xavier_normal_(self.value_projector_weight)
        init.xavier_normal_(self.output_projector_weight)


    def forward(self, query: Tensor, key: Tensor, value: Tensor, mask: Optional[Tensor] = None) -> Tensor:
        query, key, value = query @ self.query_projector_weight.T, key @ self.key_projector_weight.T, value @ self.value_projector_weight.T
        query, key, value = split(query, self.number_of_heads), split(key, self.number_of_heads), split(value, self.number_of_heads)
        heads = attention(query, key, value, mask)
        heads = concat(heads)
        return heads @ self.output_projector_weight.T

There are also implementations of the layer normalization and feed forward layers, the encoder and decoder, the transformer and some other details here: notebook

The models are in the folder model and I wrote some tests for the model in the folder tests.

The implementation is not optimized and is not intended to be used in production, but to understand the transformer model and how it works. The code is written in a way that is easy to understand and follow the steps of the model. Soon I will be adding some experiments, more tests and some other implementations of the transformer model.

Contact

If you have any questions, feel free to contact me at [email protected]