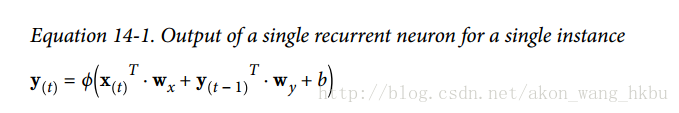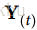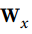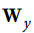Recurrent Neurons
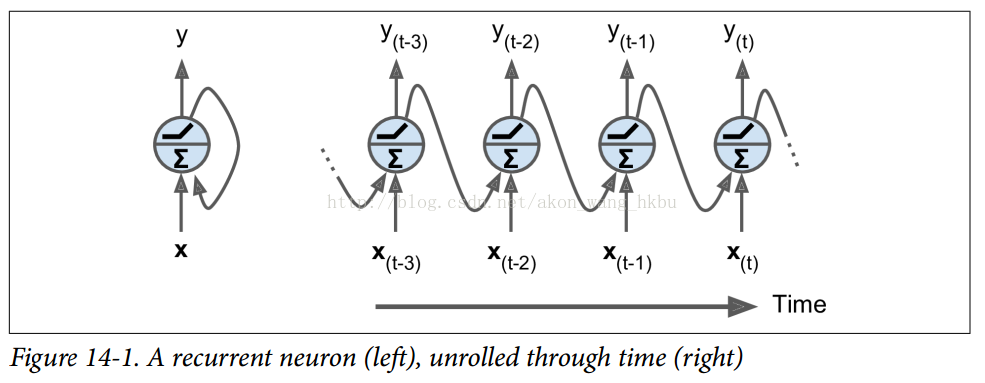
到目前为止,我们主要关注的是前馈神经网络,其中激活仅从输入层到输出层的一个方向流动(附录E中的几个网络除外)。 循环神经网络看起来非常像一个前馈神经网络,除了它也有连接指向后方。 让我们看一下最简单的RNN,它由一个神经元接收输入,产生一个输出,并将输出发送回自己,如图14-1(左)所示。 在每个时间步t(也称为一个帧),这个循环神经元接收输入x(t)以及它自己的前一时间步长y(t-1)的输出。 我们可以用时间轴来表示这个微小的网络,如图14-1(右)所示。 这被称为随着时间的推移展开网络。
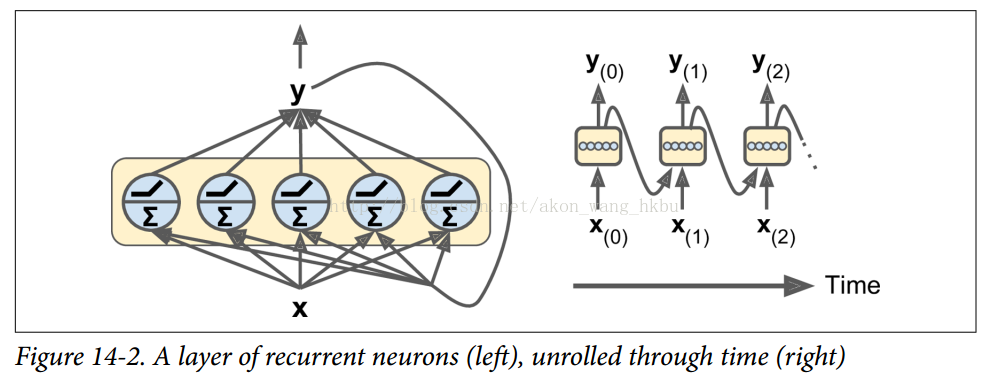
您可以轻松创建一个复发神经元层。 在每个时间步t,每个神经元都接收输入向量x(t)和前一个时间步y(t-1)的输出向量,如图14-2所示。 请注意,输入和输出都是矢量(当只有一个神经元时,输出是一个标量)。
每个循环神经元有两组权重:一组用于输入x(t),另一组用于前一时间步长y(t-1)的输出。 我们称这些权重向量为wx和wy。如方程14-1所示(b是偏差项,φ(·)是激活函数,例如ReLU),可以计算单个循环神经元的输出。
就像前馈神经网络一样,我们可以使用上一个方程的向量化形式,对整个小批量计算整个层的输出(见公式14-2)。
是一个m×n(神经元)矩阵,包含在最小批次中每个实例在时间步t处的层输出(m是最小批次中的实例数,n(神经元)是神经元)。
是包含所有实例的输入的m×n(输入)矩阵(n(输入)是输入特征的数量)。
是包含当前时间步的输入的连接权重的n(输入)×n(神经元)矩阵。
是包含当前时间步的输出的连接权重的n(输入)×n(神经元)矩阵。
- 权重矩阵Wx和Wy通常连接成形状(n(输入)+ n(神经元))×n(神经元)的单个权重矩阵W(见等式14-2的第二行)
- b是包含每个神经元的偏置项的大小为n(神经元)的向量。
注意,Y(t)是X(t)和Y(t - 1)的函数,它是X(t - 1)和Y(t - 2)的函数,它是X(t - 2)和Y(t - 3)的函数,等等。 这使得Y(t)是从时间t = 0(即X(0),X(1),...,X(t))开始的所有输入的函数。 在第一个时间步,t = 0,没有以前的输出,所以它们通常被假定为全零。
Memory Cells
由于时间t的循环神经元的输出是由所有先前时间步骤计算来的的函数,你可以说它有一种记忆形式。一个神经网络的一部分,跨越时间步长保留一些状态,称为存储单元(或简称为单元)。单个循环神经元或循环神经元层是非常基本的单元,但本章后面我们将介绍一些更为复杂和强大的单元类型。
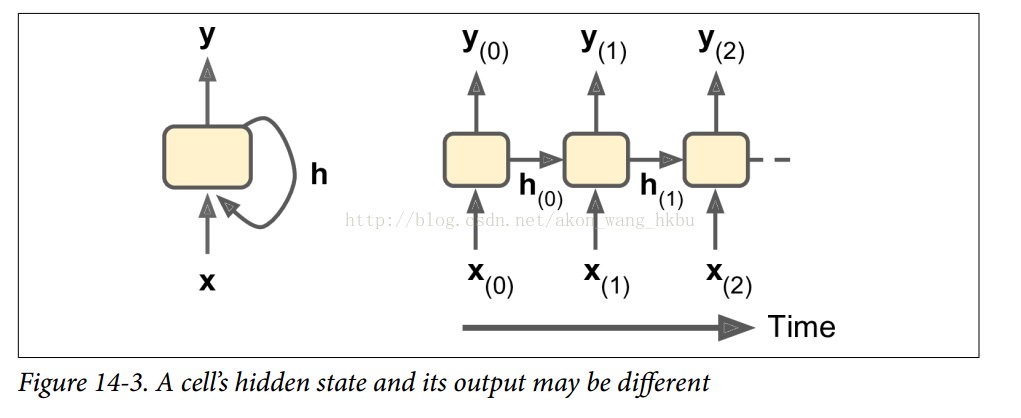
一般情况下,时间步t处的单元状态,记为h(t)(“h”代表“隐藏”),是该时间步的某些输入和前一时间步的状态的函数:h(t) = f(h(t-1),x(t))。 其在时间步t处的输出,表示为y(t),也和前一状态和当前输入的函数有关。 在我们已经讨论过的基本单元的情况下,输出等于单元状态,但是在更复杂的单元中并不总是如此,如图14-3所示。
Input and Output Sequences (输入和输出序列)
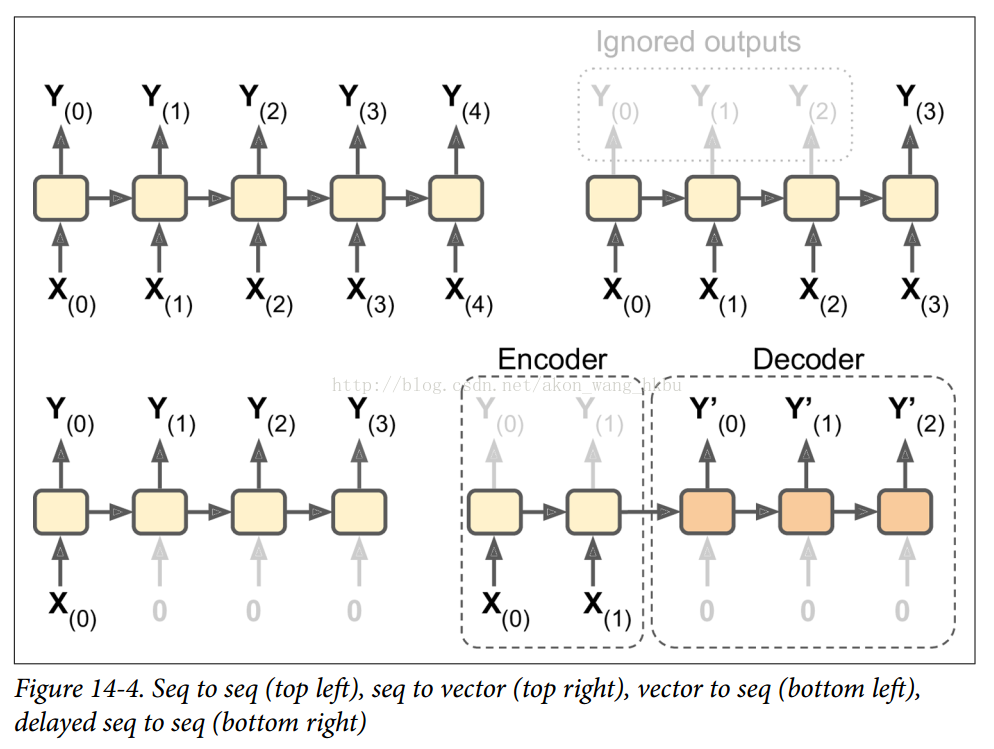
RNN可以同时进行一系列输入并产生一系列输出(见图14-4,左上角的网络)。 例如,这种类型的网络对于预测时间序列(如股票价格)非常有用:您在过去的N天内给出价格,并且它必须输出向未来一天移动的价格(即从N - 1天 前到明天)。
或者,您可以向网络输入一系列输入,并忽略除最后一个之外的所有输出(请参阅右上角的网络)。 换句话说,这是一个向量网络的序列。 例如,您可以向网络提供与电影评论相对应的单词序列,并且网络将输出情感评分(例如,从-1 [仇恨]到+1 [爱情])。
相反,您可以在第一个时间步中为网络提供一个输入(而在其他所有时间步中为零),然后让它输出一个序列(请参阅左下角的网络)。 这是一个矢量到序列的网络。 例如,输入可以是图像,输出可以是该图像的标题。
最后,你可以有一个序列到矢量网络,称为编码器,后面跟着一个称为解码器的矢量到序列网络(参见右下角的网络)。 例如,这可以用于将句子从一种语言翻译成另一种语言。 你会用一种语言给网络喂一个句子,编码器会把这个句子转换成单一的矢量表示,然后解码器将这个矢量解码成另一种语言的句子。 这种称为编码器 - 解码器的两步模型,比用单个序列到序列的RNN(如左上方所示的那个)快速地进行翻译要好得多,因为句子的最后一个单词可以 影响翻译的第一句话,所以你需要等到听完整个句子才能翻译。
Basic RNNs in TensorFlow
首先,我们来实现一个非常简单的RNN模型,而不使用任何TensorFlow的RNN操作,以更好地理解发生了什么。 我们将使用tanh激活函数创建一个由5个复发神经元层组成的RNN(如图14-2所示的RNN)。 我们将假设RNN只运行两个时间步,每个时间步输入大小为3的矢量。 下面的代码构建了这个RNN,展开了两个时间步骤:
n_inputs = 3
n_neurons = 5
X0 = tf.placeholder(tf.float32, [None, n_inputs])
X1 = tf.placeholder(tf.float32, [None, n_inputs])
Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons], dtype=tf.float32))
Wy = tf.Variable(tf.random_normal(shape=[n_neurons, n_neurons], dtype=tf.float32))
b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32))
Y0 = tf.tanh(tf.matmul(X0, Wx) + b)
Y1 = tf.tanh(tf.matmul(Y0, Wy) + tf.matmul(X1, Wx) + b)
init = tf.global_variables_initializer()
这个网络看起来很像一个双层前馈神经网络,有一些改动:首先,两个层共享相同的权重和偏差项,其次,我们在每一层都有输入,并从每个层获得输出。 为了运行模型,我们需要在两个时间步中都有输入,如下所示:
# Mini-batch: instance 0,instance 1,instance 2,instance 3
X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]]) # t = 0
X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]]) # t = 1
with tf.Session() as sess:
init.run()
Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
这个小批量包含四个实例,每个实例都有一个由两个输入组成的输入序列。 最后,Y0_val和Y1_val在所有神经元和小批量中的所有实例的两个时间步中包含网络的输出:
>>> print(Y0_val) # output at t = 0
[[-0.2964572 0.82874775 -0.34216955 -0.75720584 0.19011548] # instance 0
[-0.12842922 0.99981797 0.84704727 -0.99570125 0.38665548] # instance 1
[ 0.04731077 0.99999976 0.99330056 -0.999933 0.55339795] # instance 2
[ 0.70323634 0.99309105 0.99909431 -0.85363263 0.7472108 ]] # instance 3
>>> print(Y1_val) # output at t = 1
[[ 0.51955646 1\. 0.99999022 -0.99984968 -0.24616946] # instance 0
[-0.70553327 -0.11918639 0.48885304 0.08917919 -0.26579669] # instance 1
[-0.32477224 0.99996376 0.99933046 -0.99711186 0.10981458] # instance 2
[-0.43738723 0.91517633 0.97817528 -0.91763324 0.11047263]] # instance 3
这并不难,但是当然如果你想能够运行100多个时间步骤的RNN,这个图形将会非常大。 现在让我们看看如何使用TensorFlow的RNN操作创建相同的模型。
完整代码
import numpy as np
import tensorflow as tf
if __name__ == '__main__':
n_inputs = 3
n_neurons = 5
X0 = tf.placeholder(tf.float32, [None, n_inputs])
X1 = tf.placeholder(tf.float32, [None, n_inputs])
Wx = tf.Variable(tf.random_normal(shape=[n_inputs, n_neurons], dtype=tf.float32))
Wy = tf.Variable(tf.random_normal(shape=[n_neurons, n_neurons], dtype=tf.float32))
b = tf.Variable(tf.zeros([1, n_neurons], dtype=tf.float32))
Y0 = tf.tanh(tf.matmul(X0, Wx) + b)
Y1 = tf.tanh(tf.matmul(Y0, Wy) + tf.matmul(X1, Wx) + b)
init = tf.global_variables_initializer()
# Mini-batch: instance 0,instance 1,instance 2,instance 3
X0_batch = np.array([[0, 1, 2], [3, 4, 5], [6, 7, 8], [9, 0, 1]]) # t = 0
X1_batch = np.array([[9, 8, 7], [0, 0, 0], [6, 5, 4], [3, 2, 1]]) # t = 1
with tf.Session() as sess:
init.run()
Y0_val, Y1_val = sess.run([Y0, Y1], feed_dict={X0: X0_batch, X1: X1_batch})
print(Y0_val,'\n')
print(Y1_val)
Static Unrolling Through Time
static_rnn()函数通过链接单元格来创建一个展开的RNN网络。 下面的代码创建了与上一个完全相同的模型:
X0 = tf.placeholder(tf.float32, [None, n_inputs])
X1 = tf.placeholder(tf.float32, [None, n_inputs])
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
output_seqs, states = tf.contrib.rnn.static_rnn(basic_cell, [X0, X1],
dtype=tf.float32)
Y0, Y1 = output_seqs
首先,我们像以前一样创建输入占位符。 然后,我们创建一个BasicRNNCell,您可以将其视为一个工厂,创建单元的副本以构建展开的RNN(每个时间步一个)。 然后我们调用static_rnn(),给它的单元工厂和输入张量,并告诉它输入的数据类型(这是用来创建初始状态矩阵,默认情况下是满零)。 static_rnn()函数为每个输入调用单元工厂的__call __()函数,创建单元格的两个拷贝(每个单元包含一个5个循环神经元层),并具有共享的权重和偏置项,并且像前面一样。 static_rnn()函数返回两个对象。 第一个是包含每个时间步的输出张量的Python列表。 第二个是包含网络最终状态的张量。 当你使用基本的单元格时,最后的状态就等于最后的输出。
如果有50个时间步长,则不得不定义50个输入占位符和50个输出张量。而且,在执行时,您将不得不为50个占位符中的每个占位符输入数据并且还要操纵50个输出。我们来简化一下。下面的代码再次构建相同的RNN,但是这次它需要一个形状为[None,n_steps,n_inputs]的单个输入占位符,其中第一个维度是最小批量大小。然后提取每个时间步的输入序列列表。 X_seqs是形状n_steps张量的Python列表[None,n_inputs],其中第一个维度再次是最小批量大小。为此,我们首先使用转置()函数交换前两个维度,以便时间步骤现在是第一维度。然后,我们使 unstack()函数沿第一维(即每个时间步的一个张量)提取张量的Python列表。接下来的两行和以前一样。最后,我们使用stack()函数将所有输出张量合并成一个张量,然后我们交换前两个维度得到形状的最终输出张量[None, n_steps,n_neurons](第一个维度是mini-批量大小)。
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
X_seqs = tf.unstack(tf.transpose(X, perm=[1, 0, 2]))
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
output_seqs, states = tf.contrib.rnn.static_rnn(basic_cell, X_seqs,
dtype=tf.float32)
outputs = tf.transpose(tf.stack(output_seqs), perm=[1, 0, 2])
现在我们可以通过给它提供一个包含所有minibatch序列的张量来运行网络:
X_batch = np.array([
# t = 0 t = 1
[[0, 1, 2], [9, 8, 7]], # instance 1
[[3, 4, 5], [0, 0, 0]], # instance 2
[[6, 7, 8], [6, 5, 4]], # instance 3
[[9, 0, 1], [3, 2, 1]], # instance 4
])
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
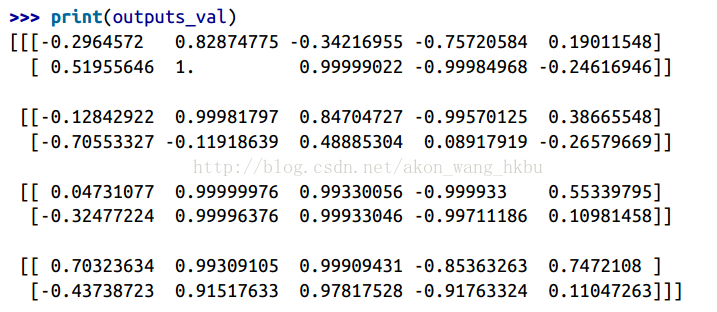
我们得到所有实例,所有时间步长和所有神经元的单一outputs_val张量:
但是,这种方法仍然会建立一个每个时间步包含一个单元的图。 如果有50个时间步,这个图看起来会非常难看。 这有点像写一个程序而没有使用循环(例如,Y0 = f(0,X0); Y1 = f(Y0,X1); Y2 = f(Y1,X2); ...; Y50 = f Y49,X50))。 如果使用大图,在反向传播期间(特别是在GPU卡内存有限的情况下),您甚至可能会发生内存不足(OOM)错误,因为它必须在正向传递期间存储所有张量值,因此可以使用它们来计算 梯度在反向通过。
幸运的是,有一个更好的解决方案:dynamic_rnn()函数。
Dynamic Unrolling Through Time
dynamic_rnn()函数使用while_loop()操作在单元格上运行适当的次数,如果要在反向传播期间将GPU内存交换到CPU内存,可以设置swap_memory = True,以避免内存不足错误。 方便的是,它还可以在每个时间步(形状[None,n_steps,n_inputs])接受所有输入的单张量,并且在每个时间步(形状[None,n_steps,n_neurons])上输出所有输出的单张量。 没有必要堆叠,拆散或转置。 以下代码使用dynamic_rnn()函数创建与之前相同的RNN。 这太好了!
完整代码
import numpy as np
import tensorflow as tf
import pandas as pd
if __name__ == '__main__':
n_steps = 2
n_inputs = 3
n_neurons = 5
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
init = tf.global_variables_initializer()
X_batch = np.array([
[[0, 1, 2], [9, 8, 7]], # instance 1
[[3, 4, 5], [0, 0, 0]], # instance 2
[[6, 7, 8], [6, 5, 4]], # instance 3
[[9, 0, 1], [3, 2, 1]], # instance 4
])
with tf.Session() as sess:
init.run()
outputs_val = outputs.eval(feed_dict={X: X_batch})
print(outputs_val)
在反向传播期间,while_loop()操作会执行相应的步骤:在正向传递期间存储每次迭代的张量值,以便在反向传递期间使用它们来计算梯度。
Handling Variable Length Input Sequences
到目前为止,我们只使用固定大小的输入序列(全部正好两个步长)。 如果输入序列具有可变长度(例如,像句子)呢? 在这种情况下,您应该在调用dynamic_rnn()(或static_rnn())函数时设置sequence_length参数; 它必须是一维张量,表示每个实例的输入序列的长度。 例如:
n_steps = 2
n_inputs = 3
n_neurons = 5
reset_graph()
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
seq_length = tf.placeholder(tf.int32, [None])
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32,
sequence_length=seq_length)
例如,假设第二个输入序列只包含一个输入而不是两个输入。 为了适应输入张量X,必须填充零向量(因为输入张量的第二维是最长序列的大小,即2)
X_batch = np.array([
# step 0 step 1
[[0, 1, 2], [9, 8, 7]], # instance 1
[[3, 4, 5], [0, 0, 0]], # instance 2 (padded with zero vectors)
[[6, 7, 8], [6, 5, 4]], # instance 3
[[9, 0, 1], [3, 2, 1]], # instance 4
])
seq_length_batch = np.array([2, 1, 2, 2])
当然,您现在需要为两个占位符X和seq_length提供值:
with tf.Session() as sess:
init.run()
outputs_val, states_val = sess.run(
[outputs, states], feed_dict={X: X_batch, seq_length: seq_length_batch})
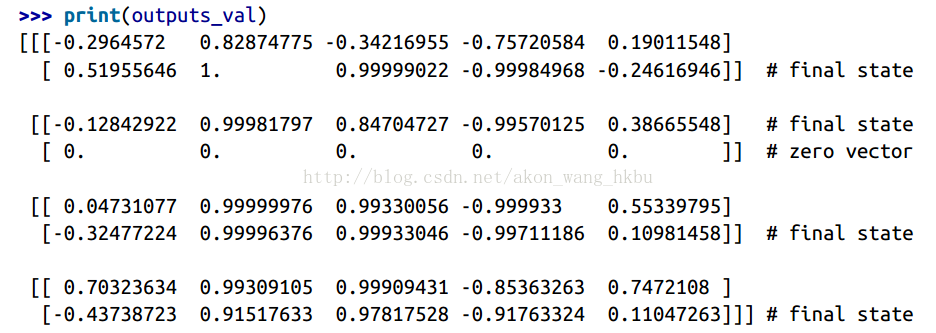
现在,RNN输出序列长度的每个时间步都会输出零矢量(查看第二个时间步的第二个输出):
此外,状态张量包含每个单元的最终状态(不包括零向量):
Handling Variable-Length Output Sequences(处理可变长度输出序列)
如果输出序列长度不一样呢? 如果事先知道每个序列的长度(例如,如果知道长度与输入序列的长度相同),那么可以按照上面所述设置sequence_length参数。 不幸的是,通常这是不可能的:例如,翻译后的句子的长度通常与输入句子的长度不同。 在这种情况下,最常见的解决方案是定义一个称为序列结束标记(EOS标记)的特殊输出。 任何通过EOS的输出应该被忽略(我们将在本章稍后讨论)。
好,现在你知道如何建立一个RNN网络(或者更准确地说是一个随着时间的推移而展开的RNN网络)。 但是你怎么训练呢?
Training RNNs
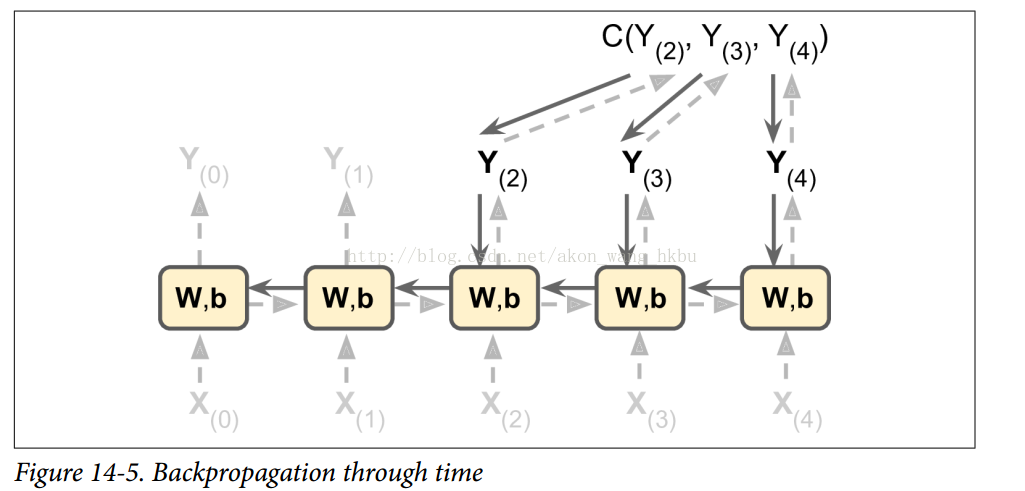
为了训练一个RNN,诀窍是通过时间展开(就像我们刚刚做的那样),然后简单地使用常规反向传播(见图14-5)。 这个策略被称为反向传播(BPTT)。
就像在正常的反向传播中一样,展开的网络(用虚线箭头表示)有第一个正向传递。 那么使用成本函数评估输出序列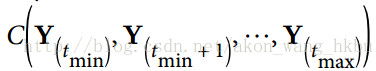
Training a Sequence Classifer (训练序列分类器)
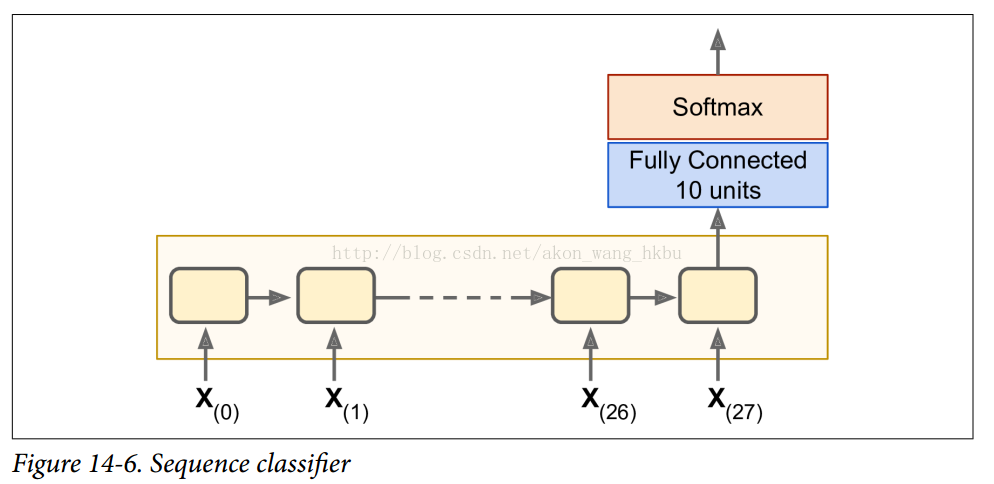
我们训练一个RNN来分类MNIST图像。 卷积神经网络将更适合于图像分类(见第13章),但这是一个你已经熟悉的简单例子。 我们将把每个图像视为28行28像素的序列(因为每个MNIST图像是28×28像素)。 我们将使用150个循环神经元的细胞,再加上一个完整的连接图层,其中包含连接到上一个时间步的输出的10个神经元(每个类一个),然后是一个softmax层(见图14-6)。
建模阶段非常简单, 它和我们在第10章中建立的MNIST分类器几乎是一样的,只是展开的RNN替换了隐藏的层。 注意,完全连接的层连接到状态张量,其仅包含RNN的最终状态(即,第28个输出)。 另请注意,y是目标类的占位符。
n_steps = 28
n_inputs = 28
n_neurons = 150
n_outputs = 10
learning_rate = 0.001
X = tf.placeholder(tf.float32, [None, n_steps, n_inputs])
y = tf.placeholder(tf.int32, [None])
basic_cell = tf.contrib.rnn.BasicRNNCell(num_units=n_neurons)
outputs, states = tf.nn.dynamic_rnn(basic_cell, X, dtype=tf.float32)
logits = tf.layers.dense(states, n_outputs)
xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=y,
logits=logits)
loss = tf.reduce_mean(xentropy)
optimizer = tf.train.AdamOptimizer(learning_rate=learning_rate)
training_op = optimizer.minimize(loss)
correct = tf.nn.in_top_k(logits, y, 1)
accuracy = tf.reduce_mean(tf.cast(correct, tf.float32))
init = tf.global_variables_initializer()
现在让我们加载MNIST数据,并按照网络预期的方式将测试数据重塑为[batch_size,n_steps,n_inputs]。 我们将立即关注重塑训练数据。
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/")
X_test = mnist.test.images.reshape((-1, n_steps, n_inputs))
y_test = mnist.test.labels
现在我们准备训练RNN了。 执行阶段与第10章中MNIST分类器的执行阶段完全相同,不同之处在于我们在将每个训练的批量喂到网络之前要重新调整。
batch_size = 150
with tf.Session() as sess:
init.run()
for epoch in range(n_epochs):
for iteration in range(mnist.train.num_examples // batch_size):
X_batch, y_batch = mnist.train.next_batch(batch_size)
X_batch = X_batch.reshape((-1, n_steps, n_inputs))
sess.run(training_op, feed_dict={X: X_batch, y: y_batch})
acc_train = accuracy.eval(feed_dict={X: X_batch, y: y_batch})
acc_test = accuracy.eval(feed_dict={X: X_test, y: y_test})
print(epoch, "Train accuracy:", acc_train, "Test accuracy:", acc_test)
输出应该是这样的:
我们获得了超过98%的准确性 - 不错! 另外,通过调整超参数,使用He初始化初始化RNN权重,更长时间训练或添加一些正则化(例如,丢失),您肯定会获得更好的结果。
您可以通过将其构造代码包装在一个变量范围内(例如,使用variable_scope(“rnn”,initializer = variance_scaling_initializer())来使用He初始化)来为RNN指定初始化器。
Training to Predict Time Series
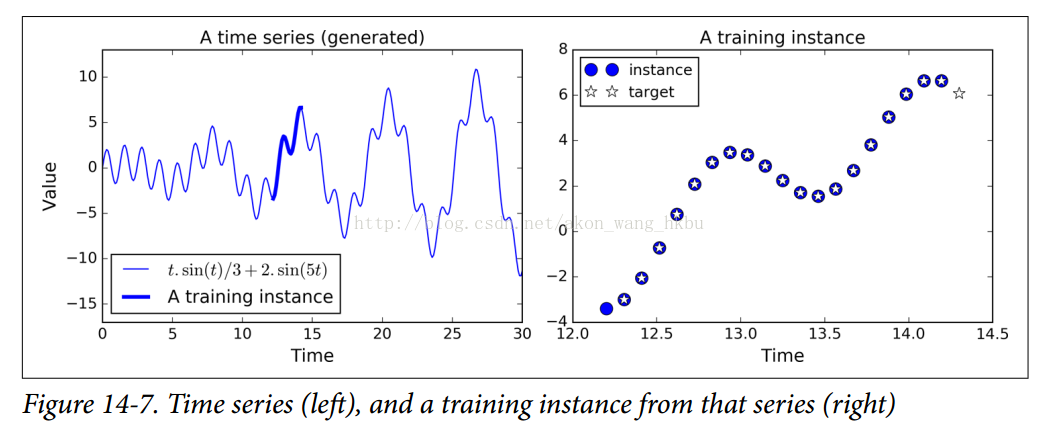
现在让我们来看看如何处理时间序列,如股价,气温,脑电波模式等等。 在本节中,我们将训练一个RNN来预测生成的时间序列中的下一个值。 每个训练实例是从时间序列中随机选取的20个连续值的序列,目标序列与输入序列相同,除了向后移动一个时间步(参见图14-7)。
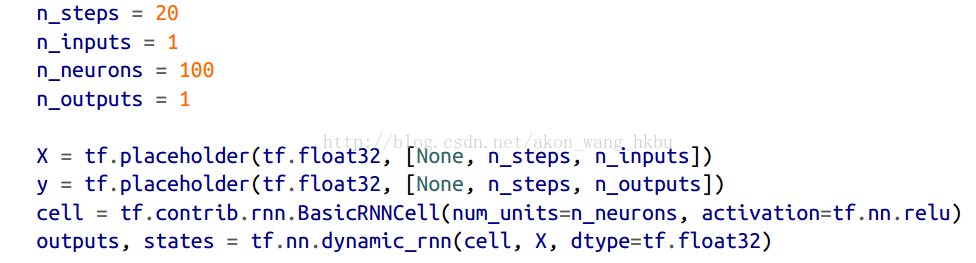
首先,我们来创建一个RNN。 它将包含100个经常性的神经元,并且我们将在20个时间步骤中展开它,因为每个训练实例将是20个输入长。 每个输入将仅包含一个特征(在该时间的值)。 目标也是20个输入序列,每个输入包含一个值。 代码与之前几乎相同:
一般来说,你将不只有一个输入功能。 例如,如果您试图预测股票价格,则您可能在每个时间步骤都会有许多其他输入功能,例如竞争股票的价格,分析师的评级或可能帮助系统进行预测的任何其他功能。
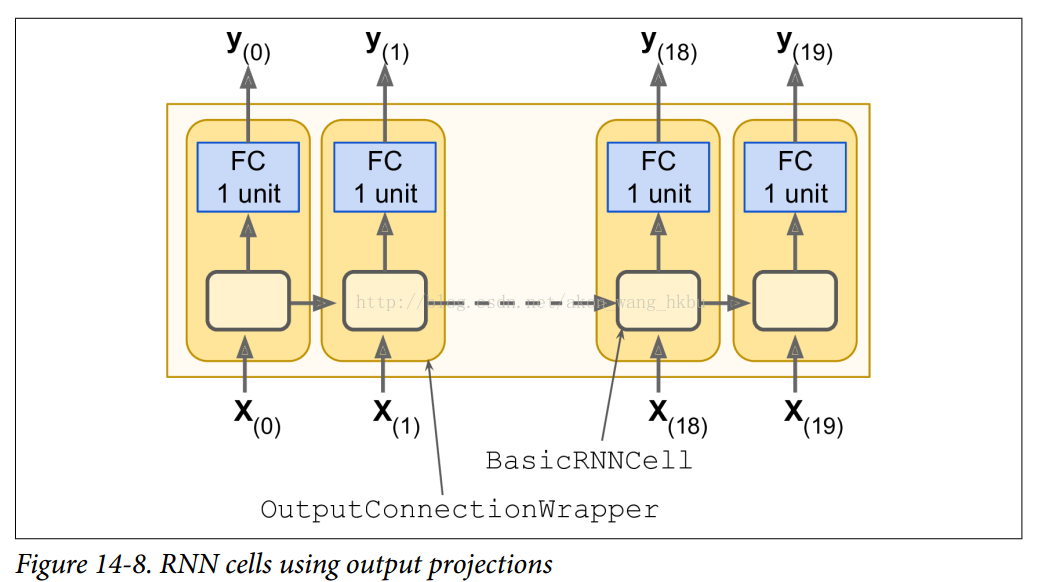
在每个时间步,我们现在有一个大小为100的输出向量。但是我们实际需要的是每个时间步的单个输出值。 最简单的解决方法是将单元格包装在OutputProjectionWrapper中。 单元格包装器就像一个普通的单元格,代理每个方法调用一个底层单元格,但是它也增加了一些功能。 Out putProjectionWrapper在每个输出之上添加一个完全连接的线性神经元层(即没有任何激活函数)(但不影响单元状态)。 所有这些完全连接的层共享相同(可训练)的权重和偏差项。 结果RNN如图14-8所示。
包装细胞是相当容易的。 让我们通过将BasicRNNCell包装到OutputProjectionWrapper中来调整前面的代码:
包装细胞是相当容易的。 让我们通过将BasicRNNCell包装到OutputProjectionWrapper中来调整前面的代码:
cell =tf.contrib.rnn.OutputProjectionWrapper(
tf.contrib.rnn.BasicRNNCell(num_units=n_neurons,activation=tf.nn.relu),
output_size=n_outputs)
到现在为止还挺好。 现在我们需要定义成本函数。 我们将使用均方误差(MSE),就像我们在之前的回归任务中所做的那样。 接下来,我们将像往常一样创建一个Adam优化器,训练操作和变量初始化操作: