PUSH NOTE : 差分约束.md

docs/数学/图论/差分约束.md

@@ -0,0 +1,104 @@
+---
+tags:
+  - no-tag
+date: 2024-09-08
+publish: true
+---
+# 差分约束
+
+## 简介
+
+差分约束系统，有 $m$ 条约束条件，每条都为形如 $x_a-x_b\geq c_k，x_a-x_b\leq c_k$ 或 $x_a=x_b$ 的形式，判断该差分约束系统有没有解，求出其解。
+
+题意转化：考虑建立最短路模型，差分约束系统中的每个约束条件 $x_i-x_j\leq c_k$ 都可以变形成 $x_i\leq x_j+c_k$，这与单源最短路中的三角形不等式 $dist[y]\leq dist[x]+z$ 非常相似（x->y）
+
+### 例题 [luogu P1993 小 K 的农场](https://www.luogu.com.cn/problem/P1993)
+
+式子 | $\leq$ | 连边
+--- | --- | ---
+$x_a - x_b \geq c$  | $x_b - x_a \leq -c$	|  `add(a, b, -c);`
+$x_a - x_b \leq c$|	$x_a - x_b \leq c$	|`add(b, a, c);`
+$x_a = x_b$	|$x_a - x_b \leq 0, \space x_b - x_a \leq 0$|	`add(b, a, 0), add(a, b, 0);`
+
+### 例题 [P4926[1007] 倍杀测量者](https://www.luogu.com.cn/problem/P4926)
+
+不考虑二分等其他的东西，差分系统 $\frac{x_i}{x_j}\leq c_k$ 的求解方法：
+
+对每个 $x_i,x_j$ 和 $c_k$ 取一个 $\log$ 就可以把乘法变成加法运算，即 $\log x_i-\log x_j \leq \log c_k$，这样就可以用差分约束解决了。
+
+## 判定无解
+
+由于 $a_i$ 是一组最短路的解，那么只需判定最短路是否无解——**判负环**
+
+ `SPFA` 判负环：每次将一个点丢进队列里，相当于是对这一个点的所有出边进行松弛，那么只需要**记录每个点的进队次数**，若超过`总节点数-1`，说明松弛次数太多，有负环，无解；否则有解。
+
+有超级源点——`incnt[to]>=n+1`时break；
+无超级源点——`incnt[to]>=n`时break。
+
+## 求解
+
+如果跑完了spfa，则最终`dis[1~n]`的数即为一组解。
+
+有推论：**设向量 $x=(x1,x2,\cdots,x_n)$为差分约束系统 $A_x\leq b$ 的一个解，设 $d$ 为任意常数，则 $x+d=(x_1+d,x_2+d,\cdots,x_n+d)$ 也是该差分约束系统的一个解。**
+
+由该推论，我们可以把或许求出的很怪异的不等式解变成正整数解，看起来更自然。
+
+---
+
+## 易错点
+
+### 1.用错算法
+
+由于 $k$ 符号不确定，所以**可能有负（正）权边**，这也是为什么我们不能使用 `dijkstra` 算法，而只能使用 `Bellman-Ford` 或 `SPFA` 求最短（长）路的原因。
+
+------------
+
+`dijkstra` **算法求最短（长）路为何不能用于负（正）权边**
+
+（如果您早就明白这是为什么，请自行跳过）
+
+以求最短路为例，`dijkstra` 算法是利用贪心思想，每次用**距离源点最近的、未讨论过的点**去更新其他点的最短距离，有点类似于 `bfs` （宽度优先搜索）。
+
+但当出现负权边时，**后面讨论的点**相较于已讨论的点，**可能会距离源点更近**，导致**已讨论的点会被更新，却不会再次拿来讨论**，此时 $O(n^2)$ 的 `dijkstra` 算法就失效了。
+
+不过，如果使用带有**堆优化**的时间复杂度为 $O(nlog_{_2}m)$ 的 `dijkstra` 算法，它会**退化成** `SPFA` **算法**，相当于将 `SPFA` 算法中的队列换成堆，时间复杂度为 $O(nmlog_{_2}m)$，显然超时。
+
+------------
+
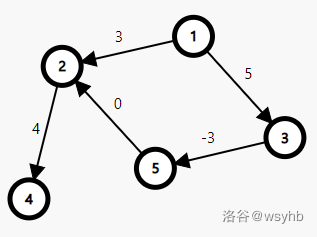
+最后放一个例子，以便读者理解：
+
+![示意图](https://cdn.luogu.com.cn/upload/image_hosting/ur7yo813.png)
+
+以 $1$ 为源点，用 $O(n^2)$ 的 `dijkstra` 算法求解单源最短路，所求得的 $dis_{_4}$ 为 $7$，即路径 $1$ -> $2$ -> $4$。而实际上 $dis_{_4}$ 应该为 $6$，即路径 $1$ -> $3$ -> $5$ -> $2$ -> $4$。
+
+错误原因是 $dis_{_2}=3<dis_{_3}=5$，所以先讨论了点 $2$ ，将点 $4$ 更新，而之后点 $5$ 去更新点 $2$，点 $2$ 却不会再用新的 $dis_{_2}=2$ 去更新点 $4$ 了。
+
+### 2.图不连通
+
+这里可能会存在**点之间既不直接约束也不间接约束**的情况，在建图上的体现就是**图不连通**。
+
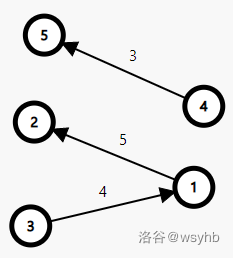
+举个简单的例子：（$n=5$，$m=3$）
+
+$$
+\begin{cases}
+x_2-x_1 \leq 5\\
+x_5-x_4 \leq 3\\
+x_1-x_3 \leq 4\\
+\end{cases}
+$$
+
+依据第一种思路建图如下：
+
+![示意图](https://cdn.luogu.com.cn/upload/image_hosting/lsk6hzvw.png)
+
+此时无论以 $1$ , $2$ , $3$ , $4$ , $5$ 哪个点作为源点，都无法计算出正确答案。（对于 `SPFA`）
+
+理由是**以其中一个点作为源点，只能计算出这个点所在连通块的答案**，并没有计算其他连通块的答案。
+
+---
+
+`SPFA`**解决方案**
+
+1. **一开始将所有点放入队列**中而不是只放一个起点，这样每个点都被作为起点讨论过。
+
+2. **建一个虚拟源点 $0$，从这个虚拟源点向其他所有点都连一条长度为 $0$ 的边，以虚拟源点为起点放入队列**，这样的效果与前一种完全相同。但是不要忘了把边开大！！！！！！