تا الان هممون حداقل یک مفهوم سطحی از data structure رو یاد گرفتیم. توی ویکی پدیا و اکثر وب سایت ها همون توضیح کوتاه رو میده.
اما بیاید یکم عمیق تر شیم
خب Structure که مشخصه یک آرایش، ساختار، سازمان دهی کردن هستش.
دیتا (Data) چیه؟
برای درک دیتا بهتره کمی درباره ساز و کار کامپیوتر بدونیم.
قلب تپنده کامپیوتر CPU هستش سی پی یو یک چیزی داره به اسم ALU کار اصلی ایشون در واقع انجام محاسبه ها و انجام عملیات های منطقی روی داده ها توی پردازنده اصلی یا همون CPU هستش.
داده ها از کجا میان ؟ داده ها از main memory یا همون رم سیستم میان. تا اونجا که خودتون در جریانید کامپیوتر ها باینری هستن پس اینطور در نظر بگیرید ما کلی صفر و یک توی رم داریم.
نکته ای که باید توجه کنید اینه کامپیوتر ذاتا فقط عدد میفهمه
اگه شما با هر زبان برنامه نویسی کار کرده باشید یک چیزی وجود داره به اسم انواع داده (data types)
هر زبان برنامه نویسی یک سری انواع داده اصلی رو میده.
اولین نوع داده ای که میشه اشاره کرد Boolean هستش. اینطوریه که اگه صفر بود false هستش و اگه غیر صفر بود true مثلا یک باشه true هستش کامپیوتر هم اینو خیلی راحت میفهمه، بیسیک ترین نوع داده هستش که با یه بیت هم میشه نمایشش داد
انواع اعداد رو داریم مثلا int، short, long
اعداد اعشاری رو داریم مثل float و double
خب تا اینجا هر نوع تایپی که اشاره کردیم عدد بود و همچنین کل چیزی که CPU میفهمه اعداد هستش
ولی خب سوال اینجاست. ما که فقط اعداد نداریم مثلا چیزی به اسم رشته (String) رو داریم. پس چطور باهاش کار می کنیم؟
رشته چطوری ساخته میشه؟ رشته به این شکل ساخته میشه که میایم بر اساس هر حرف عددی رو تعریف میکنیم. اگه یادتون باشه چیزی به اسم جدول ascii codes داریم که توی این جدول مشخص شده مثلا A میشه 65 پس چیزی که توی حافظه برای رشته نوشتیم در واقع عدد هستش
اگه همه چی عدد هستش. چجوری داده های پیچیده تر رو میسازیم؟
برای ساخت داده های پیچیده تر میتونیم از composition یعنی ترکیب کردن استفاده کنیم. یعنی میایم چند تا نوع داده رو با هم ترکیب میکنیم یک نوع داده پیچیده تر رو میسازیم.
فرض کنید میخوایم اطلاعات دانش آموز رو ذخیره کنیم. برای اینکار نیازه که ما چند توع دیتا تایپ رو با هم ترکیب کنیم تا بتونیم دانشجو رو بسازیم. مثلا دانشجو نام داره که String هستش،کد دانشجویی داره و اطلاعات دیگه. پس چیزی که ما میسازیم به این
name: str
Student code: int
age: intAggregation:
یک روش دیگه هم برای مدریت و ساخت انواع جدید، aggregation (البته چند روش دیگه هم داریم) هست. توی Aggregation یک سری از آبجکت ها، اشیا رو کنار هم قرار میدیم تا یک چیز بزرگ تری رو بسازیم
مثلا تعدادی دانشجو رو کنار هم قرار میدیم و کلاس رو میسازیم
این آبجکت هایی که کنار هم دیگه میذاریم خودشون بصورت مستقل شخصیت دارن مثلا شما دانشجو رو فرض کنید. بصورت جداگانه هم شخصیت داره اما حالا ما چیزی داریم به اسم کلاس که داخل خودش دانشجو هایی که توی کلاس هستن رو داره. به این کار که ما آبجکت های مستقل رو کنار هم میذاریم میگن تجمیع و یا Aggregation کردن.
حالا وقتی که میایم آبجکت ها رو کنار هم قرار میدیم به ساختار و آرایشی نیاز داریم که بتونیم این آبجکت ها رو کنار همدیگه قرار بدیم. اینجاست که ساختمان داده ها (Data structures) به دادمون میرسه🥰
در واقع اینجا نیاز اینکه ما باید ساختار داده ای و یا ساختار های داده داشته باشیم حس شد و داستان ما از اینجا شروع میشه.
ما انواع مختلفی از ساختمان داده داریم که هر کدومشون در جای مناسب کاربرد دارن. در ادامه چند نوع ساختمان داده رو بررسی میکنیم و مثال از نحوه پیاده کردنش توی پایتون براتون میزنم.
پایه ای ترین نوع ساختمان داده هستش. توی آرایه ما می تونیم set کنیم چیزی رو اضافه کنیم و یا get کنیم و آبجکتی رو بگیریم و تمام.
مثلا:
[1, 2, 5, 9]
set(1, 9) ---> [1, 9, 5, 9]
get(0) -----> 1آرایه ها خیلی کاربردی هستن ولی یک سری محدودیت ها و معایبی رو دارن. مثلا:
شما باید موقع تعریف کردنش مشخص کنید که چقدر طول داره. اگه بخوایم یک عنصری رو توی index مشخص شده جا بدیم در واقع insert کنیم، قابلیتش رو نداره یا اگه بخوایم عنصری رو از index مشخص پاک کنیم بازم قابلیتش رو نداره.
برای حل این مشکلات ساختمان داده ای به اسم Array list و یا تو بعضی از زبان های برنامه نویسی بهش «وکتور» میگیم که توی پایتون بهش لیست میگیم.
ساختمان داده Array list رو میتونیم با استفاده از Array پیاده کنیم.یک Array list این ویژگی هارو باید داشته باشه:
بتونیم insert, remove, add, get_size رو انجام بدیم.
همونطور که اشاره کردیم آرایه در ابتدا اینکه چقدر طول داشته باشه رو از ما میگیره و قابل تغییر دادن هم که نیسن. پس احتمالا حدس زدید کاری که انجام میدیم اینه که توی Array list اول از همه بیشتر از فضایی که نیازه رو در نظر میگیریم و خالی قرار میدیمش. بعد کاری که میکنیم اینه وقتی چیزی add میشه ما میایم تو آخر آرایه اون رو اضافه میکنیم.
اینکه آخر آرایه بلاک چندم هستش رو با استفاده از size که مشخص کردیم میفهمیم. یعنی مثلا اگه یک لیست با سه عنصر بوجود آوردیم سایزش میشه سه و اگه چیزی رو add کنیم با توجه به اینکه سایز ما سه بوده پس توی size + 1 ذخیرش میکنیم. پس در کل نحوه ساخت یک آرایه لیست به این صورت است.
توی Array list ما یک سری مشکلات رو هم داریم. مثلا خیلی از وقتا یا O(n) مواجه میشویم. برای مثال اگه size لیست ما به اندازه طولی که مشخص کرده بودیم رسید. اونوقت باید بیایم کل داده رو توی یک Array دیگه که طول بزرگ تری دارد کپی کنیم و یا زمانی که index صفر را remove میکنیم اتفاقی که می افتد این است تمامی عناصر یک index عقب تر می روند که کار ساده ای نیست.
نحوه پیاده سازی یک Array List رو بصورت عملی انجام نمیدم. بنظرم توضیحات کافیه
وقتی حرف از صف زده میشه همیشه یاد صف نونوایی بیوفتید. هر کی اول وارد شده، اولم نون میگیره. توی صف ما میگیم FIFO(First input first output) کسی که اول وارد شده اول هم خارج میشه. اما خب صف رو چجوری میتونیم پیادش کنیم؟صف رو میتونیم با استفاده از Array list پیادش کنیم. در واقع میایم از دیزاین پترن Adapter استفاده میکنیم و لیست رو سبک و سنگینش میکنیم تا برای ما کاربرد صف رو داشته باشه
صف یه سری متد ها رو باید داشته باشه. مثل:
متد add, take, head, tail, size
متد add برای اضافه کردن به صف، متد take برای گرفتن اولین نفر و برگردوندنش و حذف کردنش از صف، متد head برای نشون دادن اولین نفری که توی صفحه و متد tail برای نشون دادن آخرین نفری که توی صف قرار داره و متد size برای دیدن اینکه صف ما حالا چند نفر منتظرن داخلش.
نحوه پیاده کردن یک صف ساده توی پایتون با استفاده از لیست:
from typing import Any
class Queue(list):
def add(self, value) -> None:
self.append(value)
def size(self) -> int:
return len(self)
def get_first(self) -> Any:
try:
return self[0]
except IndexError:
raise IndexError('Queue index out of range')
def get_last(self) -> Any:
try:
return self[-1]
except IndexError:
raise IndexError('Queue index out of range')
def take(self) -> Any:
first = self.get_first()
del self[0]
return first
def head(self) -> Any:
return self.get_first()
def tail(self) -> Any:
return self.get_last()در پشته (Stack) هر کی اول بره، اول بیرون نمیاد. هر کی آخر بره اول بیرون میاد. توی پشته میگیم LILO(Last input last output) یعنی همون هر کی آخر بره اول بیرون میاد
یک سطح رو در نظر بگیرید که داخلش دیتا رو میریزیم. خب مشخصا وقتی میخوایم چیزی برداریم اونی که آخر وارد شده در دسترس هستش.
برای پیاده سازی پشته مثل صف دوباره از لیست استفاده می کنیم. متد هایی که نیازه داشته باشیم اینا هستن:
add, size, pop, top
متد add برای اضافه کردن توی پشته، متد size برای دیدن سایز، متد pop برای گرفتن و حذف کردن آخرین استفاده میشه و متد top برای دیدن اونی که آخر از همه وارد شد.
پیاده کردن یک پشته ساده با استفاده از لیست توی پایتون:
from typing import Any
class Stack(list):
def add(self, value) -> None:
self.append(value)
def size(self) -> int:
return len(self)
def get_last(self) -> Any:
try:
return self[-1]
except IndexError:
raise IndexError('Stack index out of range')
def pop(self) -> Any:
try:
return super().pop()
except IndexError:
raise IndexError('pop from empty stack.')
def top(self) -> Any:
return self.get_last()توی صف وقتی take میکنیم و اولین کسی که وارد شده رو میگریم این اتفاق میوفته:
اونی که ایندکسش مساوی با 0 هستش رو میگیریم. وقتی که حذف میکنیم همه عناصر یک ایندکس به عقب میرن. مثلا اگه صف ما سایزش یه میلیون باشه خودتون فکر کنید چقدر اینکار سربار اضافی بوجود میاره.
برای حل این مشکل ما میتونیم از لیست های پیوندی استفاده کنیم.🥳
بعد از توضیح ساختار لیست پایتون میریم سراغش...
ساختار داده ی لیست پایتون بصورت Dynamic Array و یا همون Array list هستند. به همین دلیل در مثال بالا که برای ساخت صف و پشته از لیست پایتون استفاده کردیم گفتبم که به مشکل o(n) برخورد میکنیم. چون Dynamic array ها بصورت متوالی دیتا رو ذخیره میکنن.یعنی وقتی که ما میایم ایندکس 0 رو حذف میکنیم کل عناصر لیست باید یک ایندکس به عقب بروند و یا موقعی که چیزی رو insert می کنیم باید عناصر بعد از آن ایندکس که اضافه کردیم یک ایندکس به جلو بروند و خب این خوب نیست.
البته این رو هم در نظر بگیرید در تعداد پایین و سایز کم لیست ها خیلیم عالی هستند و خیلی کاربرد داره اما در big data پیشنهاد نمی شود.
pointer:
پایتون در واقع داخل لیست ها دیتا رو ذخیره نمی کته. کاری که می کنه اینه pointer اون دیتا رو ذخیره میکنه یعنی اشاره گری که فضای دیتا رو نشون میده. اینکار سبب میشه که یه سری مزیت هارو لیست های پایتون بدست بیاره
در کتاب Hands on data structures and algorithms with Python اینگونه توضیح داده:
Contrary to arrays, pointer structures are lists of items that can be spread out in memory. This is because each item contains one or more links to other items in the structure. The types of these links are dependent on the type of structures we have. If we are dealing with linked lists, then we will have links to the next (and possibly previous) items in the structure. In the case of a tree, we have parent-child links as well as sibling links. There are several benefits to pointer structures. First of all, they don't require sequential storage space. Secondly, they can start small and grow arbitrarily as you add more nodes to the structure. However, this flexibility in pointers comes at a cost. We need additional space to store the address. For example, if you have a list of integers, each node is going to take up space by storing an integer, as well as an additional integer for storing the pointer to the next node
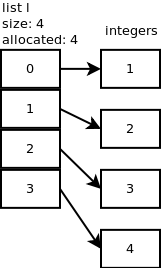
در این قسمت با چند مثال نحوه کارکرد لیست رو در Cpython بررسی میکنیم.قبل از هرچیزی باید معنی size لیست و allocated slots رو بدونید. size در واقع همون مقدار عناصر داخل لیستمون هستش که با len() میشه بدستش آورد. اما allocated slots مقدار فضایی که موقع ساخن array اختصاص دادیم هستش. همونطور که میدونید لیست پایتون در واقع یک Dynamic array هستش که در نهایت به array می رسد.
ساختن لیست: فرض کنید ما یک لیست حالی میسازیم. در این صورت allocated size ما مساوی با 0 است.
عملیات append:
اول از همه چک میشود که size لیست از allocated کوچک تر باشد و اگر مساوی بود آرایه رو resize میکنه و یک آرایه بزرگ تر می سازد. برای resize کردن یک فرمولی براش داره مثل زیر:
The growth pattern of the list is: 0, 4, 8, 16, 25, 35, 46, 58, 72, 88, …
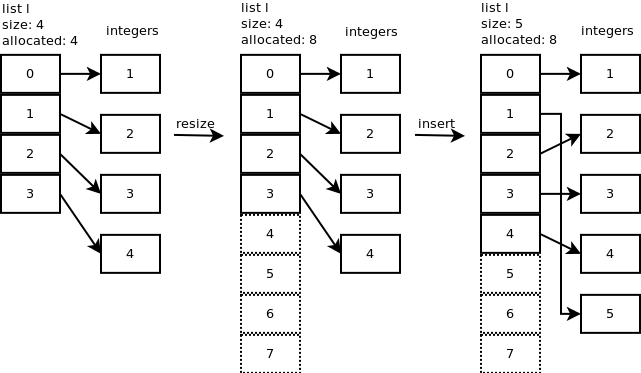
پس الان لیست ما allocated slots مساوی با 4 هستش. یعنی اگه عملیات append رو تا 4 بار انجام بدیم بصورت o(1) انجام میشود
لیست ما الان allocated مساوی با 4 هستش و size هم مساوی با چهار. در عملیات insert که میخوایم انجام بدیم اول از همه لیست ما resize میشه و allocated slots مساوی با 8 میشه و سپس عملیات insert به شکل زیر انجام میشه.
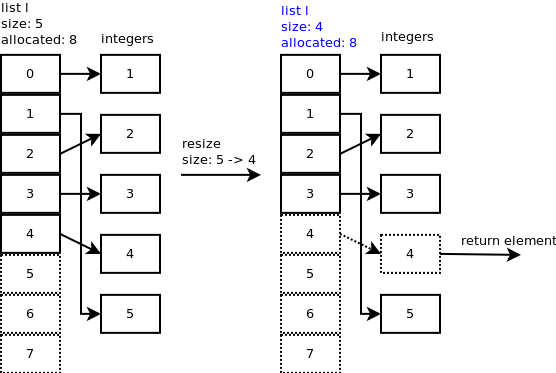
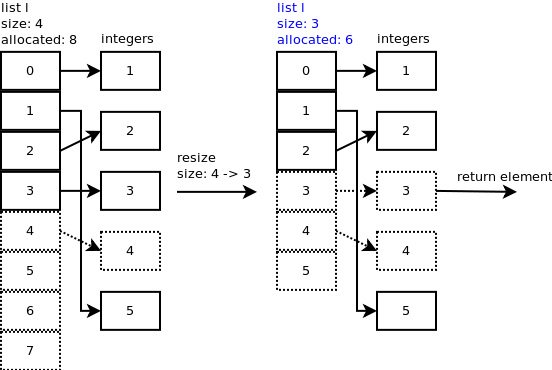
عملیات pop و remove:
در عملیات remove و pop کردن دقیقا چیزی شبیه به insert اتفاق می افتد با این تفاوت عنصر آن ایندکسی که اشاره میکنیم حذف میشود و عناصر بغد آن یک ایندکس به عقب می روند.
ما در Array داده هارا بصورت متوالی ذخیره می کردیم. یعنی داده ها کاملا چسبیده به هم ذخیره می شدند و اگه میخواستیم عملیاتی مثل insert رو انجام بدیم، مجبور میشدیم تمامی عناصر بعدش رو جابجا کنیم.
اما در لیست های پیوندی اینکار لازم نیست و insert و append و remove همیشه با n(1) انجام میشود.
لیست های پیوندی چگونه عمل می کنند؟
لیست های پیوندی در واقع تشکیل شده از composition هایی هستند که در ساده ترین حالت در خود این مقادیر را دارند:
مقدار value دیتایی که ذخیره کریدم و مقدار next که مکان عنصر بعدی را درونش ذخیره میکنیم.
همچنین هر لیست پیوندی دو مقدار head و tail را دارد که اول لیست و آخر لیست را مشخص می کند.
خب احتمالا تا الان حدس زده باشید که در لیست های پیوندی بدست آوردن سایز o(n) هستش و همچنین get کردن و set کردن در یک ایندکس هم o(n) هست.
البته می توان size را در کنار head و tail ذخیره کرد تا n(1) شود امابرای بدست آوردن یک ایندکس هیچ چاره ای نداریم و با o(n) مواجه میشویم.
معایب لیست های پیوندی به یکیش اشاره کردم که گرفتن سایز و یا یک ایندکس o(n) هستش. یکی دیگر از معایبش این است که فضای بیشتری نسبت به Array ها می گیرد. اما اگه دقت کرده باشید برای صف و پشته خیلی گزینه مناسب تری هستند تا Array ها.
لیست های پیوندی (Linked lists) دو نوع اصلی دارد. یکی از آنها Singly linked list و دیگری Doubly linked list است. تفاوت این دو با هم در مقادیری هست که ذخیره میکنند.در Singly linked list ما فقط next را ذخیره میکنیم. این باعث میشود که نتوانیم بصورت معکوس لیست را پیمایش کنیم و هر لیست مقدار قبل از خودش را نمی داند.
اما در Doubly linked list بجز next ما مقدار previous را ذخیره میکنیم یعنی هم به مقدار بعد و همچنین به مقدار قبلش دسترسی داریم.
همچنین دو نوع دیگر از لیست های پیوندی به نام های Circular linked lists و Circular doubly linked lists را داریم که اگر علاقه مند هستید درباره اش بخوانید. اما دو نوع پرکاربرش رو با هم دیگه توی پایتون پیاده می کنید.
با توجه به توضیحاتی که دادیم، یک Singly linked list در پایتون پیاده میکنیم.توجه:
یک سری مشکلات در کد من وجود دارد و صرفا مثالی از نحوه پیاده کردنش زدم. اگه دوست دارید میتونید اصلاحش کنید و ریکوئست بزنید.
from typing import Any
class Node:
def __init__(self, data):
self.data = data
self.next = None
def __str__(self):
return f'data: {self.data}'
class SinglyLinkedList:
def __init__(self) -> None:
self.__head = None
self.__tail = None
self.__size = 0
def size(self) -> int:
return self.__size
def __update_size(self) -> None:
self.__size += 1
def insure_index(self, index: int) -> None:
if index > self.size() - 1:
raise IndexError
def head(self) -> Node:
return self.__head
def tail(self) -> Node:
return self.__tail
def __set_head(self, node: Node) -> None:
self.__head = node
def __set_tail(self, node: Node) -> None:
self.__tail = node
def append(self, data: Any) -> None:
new_node = Node(data=data)
if self.head() is None:
self.__set_head(node=new_node)
if self.tail() is None:
self.__set_tail(node=new_node)
else:
self.tail().next = new_node
self.__set_tail(node=new_node)
self.__update_size()
def get_node(self, index: int) -> Node:
self.insure_index(index=index)
count = 0
current = self.head()
while index != count:
current = current.next
count += 1
return current
def get(self, index: int) -> Any:
node = self.get_node(index=index)
return node.data
def set(self, index: int, data: Any) -> None:
self.insure_index(index=index)
count = 0
current = self.head()
while index != count:
current = current.next
count += 1
current.data = data
def remove(self, index: int) -> None:
self.insure_index(index=index)
count = 0
previous = None
current = self.head()
while index != count:
previous = current
current = current.next
count += 1
if previous:
previous.next = current.next
else:
self.__set_head(current.next)
del current
def pop(self, index: int = 0) -> Any:
self.insure_index(index=index)
count = 0
previous = None
current = self.head()
while index != count:
previous = current
current = current.next
count += 1
if previous:
previous.next = current.next
else:
self.__set_head(node=current.next)
data = current.data
del current
return data
def __str__(self) -> str:
my_list = []
current = self.head()
while current:
my_list.append(current.data)
current = current.next
return str(my_list)برای مثال از نحوه پیاده سازیش توی پایتون این تکه کد رو زدم، خوشحال میشم برای کامل کردن و بهتر شدنش کمکم کنید.
from typing import Any
class Node:
def __init__(self, data: Any) -> None:
self.data = data
self.next = None
self.pre = None
def __str__(self):
return f'data: {self.data}'
class DoubleLinkedList:
def __init__(self) -> None:
self.__head = None
self.__tail = None
self.__size = 0
def size(self) -> int:
return self.__size
def __update_size(self) -> None:
self.__size += 1
def insure_index(self, index: int) -> None:
if index > self.size() - 1:
raise IndexError
def head(self) -> Node:
return self.__head
def tail(self) -> Node:
return self.__tail
def __set_head(self, node: Node) -> None:
self.__head = node
def __set_tail(self, node: Node) -> None:
self.__tail = node
def append(self, data: Any) -> None:
new_node = Node(data=data)
if self.head() is None and self.tail() is None:
self.__set_head(node=new_node)
self.__set_tail(node=new_node)
self.__update_size()
return
self.tail().next = new_node
new_node.pre = self.tail()
self.__set_tail(node=new_node)
self.__update_size()
def get_node(self, index: int) -> Node:
self.insure_index(index=index)
count = 0
current = self.head()
while index != count:
current = current.next
count += 1
return current
def get(self, index: int) -> Any:
node = self.get_node(index=index)
return node.data
def remove(self, index: int) -> None:
current = self.get_node(index=index)
if current.pre:
current.pre.next = current.next
else:
self.__set_head(node=current.next)
if current.next:
current.next.pre = current.pre
else:
self.__set_tail(node=current.pre)
del current
def insert(self, index: int, data: Any) -> None:
current = self.get_node(index=index)
new_node = Node(data=data)
new_node.next = current
new_node.pre = current.pre
if current.next:
pass
if current.pre:
current.pre.next = new_node
else:
self.__set_head(node=new_node)
self.__update_size()
def pop(self):
if self.tail():
if self.tail().pre:
self.tail().pre.next = None
self.__set_tail(node=self.tail().pre)
data = self.tail().data
else:
data = self.tail().data
self.__head = None
self.__tail = None
return data
return ValueError('Double linked list is empty.')
def __str__(self) -> str:
my_list = []
current = self.head()
while current:
my_list.append(current.data)
current = current.next
return str(my_list)برای توضیح الگوریتم مرتب سازی من توضیح ویکی پدیا رو قرار میدم و در ادامه چند تا الگوریتم مرتب سازی رو با هم پیاده می کنیم.
الگوریتم مرتبسازی، در دانش رایانه و ریاضی، الگوریتمی است که فهرستی از دادهها را به ترتیبی مشخص میچیند.
پرکاربردترین ترتیبها، ترتیبهای عددی و واژهنامهای هستند. مرتبسازی کارا در بهینهسازی الگوریتمهایی که به فهرستهای مرتب شده نیاز دارند (مثل جستجو و ترکیب)، اهمیت زیادی دارد.
از آغاز علم رایانه مسائل مرتبسازی بررسیهای فراوانی را متوجه خود ساختند؛ شاید به این علت که در عین ساده بودن، حل آن به صورت کارا پیچیده است. برای نمونه مرتبسازی حبابی در سال ۱۹۵۶ به وجود آمد. در حالی که بسیاری این را یک مسئلهٔ حل شده میپندارند، الگوریتم کارآمد جدیدی همچنان ابداع میشوند (مثلاً مرتبسازی کتابخانهای در سال ۲۰۰۴ مطرح شد).
مبحث مرتبسازی در کلاسهای معرفی علم رایانه بسیار پرکاربرد است؛ مبحثی که در آن وجود الگوریتمهای فراوان به آشنایی با ایدههای کلی و مراحل طراحی الگوریتمهای گوناگون کمک میکند؛ مانند تحلیل الگوریتم، دادهساختارها، الگوریتمهای تصادفی، تحلیل بدترین و بهترین حالت و حالت میانگین، هزینهٔ زمان و حافظه، و حد پایین.
در این الگوریتم ما به این شکل عمل می کنیم که خونه به خونه و ایندکس به ایندکس مرتب کردن رو انتجام میدهیم.یعنی اول بررسی میکنیم که کوچ ترین عدد چیست و در ایندکس صفر قرارش میدیم و بعدش بررسی میکنیم کوچک ترین برای ایدکس اول کدام عدد است و ...
این نوع مرتب سازی inplace هستش. یعنی برای sort نیازی نیست که آرایه جدیدی بوجود بیاریم و توی همون حافظه و آرایه ای که هست کار خودشو انجام میده.
unsorted_list = [10, 5, 8, 4, 6, 1, 3, 7, 2, 9, -1]
print(unsorted_list)
for i in range(len(unsorted_list)):
min_index = i
for j in range(i + 1, len(unsorted_list)):
if unsorted_list[j] < unsorted_list[min_index]:
min_index = j
(unsorted_list[i], unsorted_list[min_index]) = (unsorted_list[min_index], unsorted_list[i])
print(unsorted_list)این الگوریتم به این صورت عمل میکند که تمام عناصر لیست را یکی یکی برمیدارد و آن را در موقعیت مناسب در بخش مرتب شده قرار میدهد. انتخاب عنصر مورد نظر، اختیاری است و میتواند توسط هر الگوریتم انتخابی، انتخاب شود. مرتبسازی درجی به صورت درجا عمل میکند. نتیجه عمل بعد از k مرحله، حاوی k عنصر انتخاب شده به صورت مرتب شدهاست.
معمولترین نسخه از این الگوریتم که روی آرایهها عمل میکند، به این صورت است:
فرض کنید یک تابع به اسم Insert داریم که داده را در بخش مرتب شده در ابتدای آرایه درج میکند. این تابع با شروع از انتهای سری شروع به کار میکند و هر عنصر را به سمت راست منتقل میکند تا وقتی که جای مناسب برای عنصر جدید پیدا شود. این تابع این اثر جانبی را دارد که عنصر دقیقاً بعد از بخش مرتب شده را رونویسی میکند. برای اعمال مرتبساز درجی، از انتهای سمت چپ آرایه شروع میکنیم و با صدا زدن تابع insert، هر عنصر را به موقعیت درستش میبریم. آن بخشی که عنصر فعلی را در آن میکنیم، در ابتدای آرایه و در اندیسهایی است که آنها را قبلاً آزمایش کردهایم. هر بار صدا زدن تابع insert، یک عنصر را رونویسی میکند، اما این مسئله مشکلی ایجاد نمیکند، زیرا این داده، همانی است که الان در حال درج آن هستیم.
unsorted_list = [10, 5, 8, 4, 6, 1, 3, 7, 2, 9, -1]
for i in range(1, len(unsorted_list)):
temp = unsorted_list[i]
j = i - 1
while j >= 0 and temp < unsorted_list[j]:
unsorted_list[j + 1] = unsorted_list[j]
j -= 1
unsorted_list[j + 1] = temp
print(unsorted_list)unsorted_list = [10, 5, 8, 4, 6, 1, 3, 7, 2, 9, -1]
print(unsorted_list)
for _ in range(1, len(unsorted_list)):
for j in range(0, len(unsorted_list) - 1):
if unsorted_list[j] > unsorted_list[j + 1]:
unsorted_list[j], unsorted_list[j + 1] = unsorted_list[j + 1], unsorted_list[j]
print(unsorted_list)همونظور که از اسمش پیداست در این نوع ساختار داده ما یک ریشه (root) داریم و این ریشنه می تواند فرزندانی رو داشته باشند. همچنین فرزندان هم می توانند فرزندی رو برای خودشون داشته باشن اما هر فرزند فقط و فقط یک ریشه دارد.
ریشه:
با توجه به عکس ریشه شماره دو میشود. ریشه خودش پدر ندارد و بالاتر از همه قرار میگیره
گره میانی:
با توجه به عکس 9و 12و 8و ... گره میانی به حساب می آیند. با اینکه خودشان فرزند هستند اما خودشان هم فرزند هایی رو دارند.
برگ:
برگ به فرزندی اشاره داره که خودش فرزندی ندارد و به قول معروف شجره نامه تو این قسمت تموم میشه.
عمق:
اگر عمق ریشه را 0 در نظر بگیریم، عمق 9 برابر با 1 است و عمق 2 برابر با 2 می شود. عمیق به مکان قرارگیری نسبت به ریشه اشاره دارد که هرچقدر به ریشه نردیک تر باشد عمق نیز کمتر میشود.
همچنین ما انواع مختلفی از درخت هارو داریم مثل Binary tree و B-tree که در ادامه بصورت جزئی بررسی میکنیم.
با توجه به توضیحاتی که دادیم. یک ساختار درختی ریشته و فرزندانی را دارد. در یک مثال ساده پایتونی به این شکل می توانیم پیاده سازی کنیم:from typing import Any
class TreeNode:
def __init__(self, value: Any, parent: Any | None = None) -> None:
self.parent = parent
self.value = value
self.__children = []
def add_child(self, value) -> None:
new_child = TreeNode(value=value, parent=self)
self.__children.append(new_child)
def children(self) -> list:
return self.__children
def get_all_children(self) -> list:
all_children = []
depth_count = 0
for child in self.__children:
depth_count += 1
all_children.append(child)
all_children.extend(child.get_all_children())
return all_children
def depth(self) -> int:
count = 0
node = self
while node and node.parent:
node = node.parent
count += 1
return count
def get_depth(self) -> int:
if not self.__children:
return 0
else:
child_depths = [child.get_depth() for child in self.__children]
return max(child_depths) + 1
def get_height(self) -> int:
if not self.__children:
return 0
else:
child_heights = [child.get_height() for child in self.__children]
return max(child_heights) + 1
def remove(self) -> None:
parent = self.parent
children = self.children()
if parent:
parent.__children.extend(children)
parent.__children.remove(self)
del self
class Tree:
def __init__(self, value: Any) -> None: self.__root = self.__create_root(value=value)
@staticmethod
def __create_root(value: Any) -> TreeNode: return TreeNode(value=value)
@property
def root(self):
return self.__root
def __str__(self): return f'root name: {self.__root.value}'در پیاده سازی ساختار داده ی درختی خیلی از الگوریتم بازگشتی استفاده میشود.