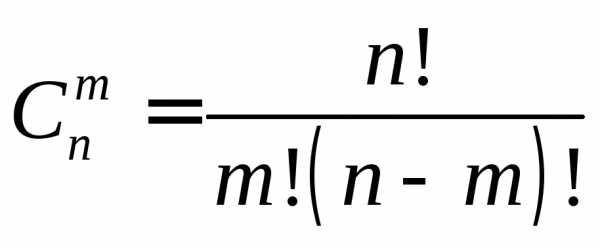Skip to content

Home

Jump to bottom
Mikhail Ostashchenko edited this page Sep 25, 2022 · 4 revisions

Math-Algorithms

🇺🇸 Math library with algorithms for c++
🇷🇺 Библиотека с++ с математическими алгоритмами


🇺🇸 Attention!!! Any function should be used with namespace mathAlgo::
🇷🇺 Внимание!!! Любую функцию нужно с использовать с пространством имён mathAlgo::


🇺🇸 Navigation:

🇷🇺 Навигация:


🇺🇸 English category

Simple arithmetic

  • Prime number

bool isPrime(uint64_t number)

The function takes as its input argument the number to be checked. The function returns true if the number is prime and false if it is composite.


Arithmetic and geometric progressions

  • N-th term of the arithmetic progression

long double nTermOfASequence(long double a1, long double d, uint64_t n)

The function takes as input arguments the first element of the progression - a1, the difference - d and the number of the sought element - n. The function returns the value of the nth element.


  • Sum of members of an arithmetic progression

long double sumAprogression(long double a1, long double an, uint64_t n)

The function takes as input arguments the first element of the progression - a1, the value of the nth element - an and the number of elements - n. The function returns the sum of the members of the sequence.


  • N-th term of the geometric progression

long double nTermOfGSequence(long double a, long double q, uint64_t n)

The function takes as input arguments the first element of the progression - a, the denominator of the progression - q and the number of the element sought - n. The function returns the value of the nth element.


  • Sum of members of a geometric progression

long double sumGprogression(long double a1, long double an, long double q)

The function takes as input arguments the first element of the progression - a1, the value of the nth element - an and the denominator - q. The function returns the sum of the members of the sequence.


Probability Theory and Combinatorics

  • Factorial

uint64_t fac(uint64_t number)

As an input argument, the function takes the number to be raised to the factorial. The function returns the factorial of the entered number.


  • Probability

long double prob(long double m, long double n)

As input arguments m takes the number of favorable outcomes, n takes the total number of test outcomes. The function returns the probability of the event.


  • Placement (order is important)

uint64_t comA(uint64_t m, uint64_t n)

Placemnt

As input arguments m and n, an ordered set of m different elements from some set of different n elements. It is important that n > m. The function returns the number of placements.


  • Combination (order is NOT important)

uint64_t comC(uint64_t m, uint64_t n)

Combination

As input arguments m and n, a set of m elements chosen from the n element set, which does not take into account the order of elements. It is important that n > m. The function returns the number of combinations.


  • Bernoulli formula

long double bern(uint64_t n, uint64_t k, long double p)

As input arguments the function takes n - total number of trials, k - number of favorable trials, p - chance of favorable outcome. The function returns the probability of a given event.


  • Local Phi number

long double fiLocal(long double x)

The function takes x - any number as an input argument. The function returns the value of the local number Phi from the given number.


  • The Phi number for the Laplace integral formula

long double fiIntegral(long double x)

The function takes x - any number as an input argument. The function returns the value of Phi from the given number for the Laplace integral formula.


  • The finite part of the function for the number of the Laplace integral formula

 double endLaplaceTheorem(double x)

The function takes x - any number as an input argument. The function returns a finite number in the Laplace integral formula. Comment: A useful practical application of this function is in calculations in the Laplace integral formula.


  • Laplace's local theorem

long double lLaplace(long double n, long double k, long double p)

As input arguments the function takes n - total number of trials, k - number of favorable trials, p - chance of favorable outcome. The function returns the probability of a given event.


  • Laplace integral theorem

long double iLaplace(long double k1, long double k2, long double n, long double p)

As input arguments the function takes k1 - number of times at least the event will occur, k2 - number of times at most the event will occur, n - total number of trials, p - chance of favorable outcome. The function returns the probability of a given event.


  • Dispersion

template <typename typeArr1, typename typeArr2>
long double dispersion(typeArr1* x, typeArr2* p, const int size)

As input arguments the function takes x - pointer to the first element of the array of random variables, p - pointer to the first element of the array of probabilities of random variables, size - size of one of the arrays. The function returns the variance of the value. Important: The size of both arrays must be the same.


  • Standard deviation of the variance from a random variable

template <typename typeArr1, typename typeArr2>
long double sDev(typeArr1* x, typeArr2* p, const int size)

As input arguments the function takes x - pointer to the first element of the array of random variables, p - pointer to the first element of the array of probabilities of random variables, size - size of one of the arrays. The function returns the variance deviation from a random variable. Important: The size of both arrays must be the same.


Numerical methods for solving nonlinear equations

  • Half-division method

template<typename F>
long double halfDivisionMethod(F func, long double a, long double b, long double e = 0.001)

The function takes as input arguments the equation func, the left and right limits of the interval a & b and the optional precision parameter e. The function returns the root of the equation on a given interval, with a given accuracy.

Example of usage:

double f(double x)
{
  return (tan(0.3 * x + 0.4) - pow(x, 2));
}

int main
{
  cout << "halfDivisionMethod: " << mathAlgo::halfDivisionMethod(&f, 0, 2) << endl;
}

Output:

halfDivisionMethod: 0.88623

  • Secant method

template<typename F>
long double secantMethod(F func, long double x0, long double x1, long double e = 0.001)

The function takes as input arguments the equation func, the left and right limits of the interval x0 & x1 and the optional precision parameter e. The function returns the root of the equation on a given interval, with a given accuracy.

Example of usage:

double f(double x)
{
  return (tan(0.3 * x + 0.4) - pow(x, 2));
}

int main
{
  cout << "secantMethod: " << mathAlgo::secantMethod(&f, 0, 2) << endl;
}

Output:

secantMethod: 0.886345

  • Parabola method

template<typename F>
long double parabolaMethod(F func, long double a, long double b, long double e = 0.001)

The function takes as input arguments the equation func, the left and right limits of the interval a & b and the optional precision parameter e. The function returns the root of the equation on a given interval, with a given accuracy.

Example of usage:

double f(double x)
{
  return (tan(0.3 * x + 0.4) - pow(x, 2));
}

int main
{
  cout << "parabolaMethod: " << mathAlgo::parabolaMethod(&f, 0, 2) << endl;
}

Output:

parabolaMethod: 0.886345

Recursive algorithms

  • Fibonacci number

uint64_t fibonacci(uint64_t n)

The function takes the number n as an input argument. The function returns the value of the Fibonacci sequence in the given position.


Geometry

  • Cotangent

long double cot(long double number)

The function takes as its input argument the number whose cotangent is to be obtained. The function returns the cotangent of the entered number.


  • Arcotangent

long double acot(long double number)

The function takes as its input argument the number number whose arcotangent is to be obtained. The function returns the arc tangent of the entered number.


  • Calculating the length of the segment

long double lengthOfLine(long double x1, long double x2, 
                         long double y1, long double y2, 
                         long double z1 = 0, long double z2 = 0)

The function takes the coordinates of points A(x1, y1) & B(x2, y2) as input arguments (z coordinates are entered for a three-dimensional coordinate system). The function returns the length of the segment.


Working with arrays and matrices

  • Finding the minimum value in an array

template <typename typeArr>
typeArr aMin(typeArr* arr, const int size)

As an argument arr is taken an array, size is the size of the array. Returns the minimum element of the array.


  • Finding the maximum value in an array

template <typename typeArr>
typeArr aMax(typeArr* arr, const int size)

As an argument arr is taken an array, size is the size of the array. Returns the maximum element of the array.


  • Sorting an array using the bubble method

template <typename typeArr>
typeArr* bSort(typeArr* arr, const int size, bool asc = true)

The function takes arr - pointer to the beginning of the array, size - size of the array, the argument asc is optional, by default true - ascending sorting, false - descending sorting. The function returns a pointer to the first element of the sorted array.


  • The average value of the array

template<typename typeArr>
typeArr avgArr(typeArr* arr, const int size)

As an argument arr is taken an array, size is the size of the array. Returns the average value of the array.


  • The mode of the array

template <typename typeArr>
typeArr modenum(typeArr* arr, const int size)

As an argument arr is taken an array, size is the size of the array. Returns the most frequent number.


  • The median of the array

template<typename typeArr>
typeArr median(typeArr* arr, const int size)

As an argument arr is taken an array, size is the size of the array. Returns the median of the array.


  • Summing two arrays

template <typename typeArr>
typeArr* sumArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

As input arguments the function takes arr0 and arr1 - pointers to the beginning of the arrays, arr2 - pointer to the first element of the array in which the previous two are summed, size - size of the arrays (the same for three). The function returns a pointer to the first element of the modified array.


  • The difference between the two arrays

template <typename typeArr>
typeArr* minArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

As input arguments the function takes arr0 and arr1 - pointers to the beginning of arrays, arr2 - pointer to the first element of the array, which will be the difference of two previous arrays, size - size of arrays (the same for three). Important: The difference of elements works on the principle: the element of the first array - the element of the second array. The function returns a pointer to the first element of the modified array.


  • Multiplying two arrays

template <typename typeArr>
typeArr* mulArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

As input arguments the function takes arr0 and arr1 - pointers to the beginning of arrays, arr2 - pointer to the first element of the array in which the previous two will be multiplied, size - size of arrays (the same for three). The function returns a pointer to the first element of the modified array.


  • Dividing two arrays

template <typename typeArr>
typeArr* divArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

As input arguments the function takes arr0 and arr1 - pointers to the beginning of the arrays, arr2 - pointer to the first element of the array, which will divide the two previous arrays, size - size of the arrays (the same for three). The function returns a pointer to the first element of the changed array. Important: The division of elements works according to the principle: element of the first array / element of the second array.


  • Adding a number to all elements of an array

template <typename typeArr, typename typeNum>
typeArr* inPlusArr(typeArr* arr, const int size, typeNum number)

As input arguments the function takes arr - pointer to the beginning of the array, size - size of the array, number - number to be added to all elements. The function returns a pointer to the first element of the modified array.


  • Subtracting a number from all elements of an array

template <typename typeArr, typename typeNum>
typeArr* inMinArr(typeArr* arr, const int size, typeNum number)

As input arguments the function takes arr - pointer to the beginning of the array, size - size of the array, number - number to be subtracted from all elements. The function returns a pointer to the first element of the modified array.


  • Multiplying all elements of the array by a number

template <typename typeArr, typename typeNum>
typeArr* inMulArr(typeArr* arr, const int size, typeNum number)

As input arguments the function takes arr - pointer to the beginning of the array, size - size of the array, number - number to be multiplied by all elements of the array. The function returns a pointer to the first element of the modified array.


  • Dividing all elements of an array by a number

template <typename typeArr, typename typeNum>
typeArr* inDivArr(typeArr* arr, const int size, typeNum number)

As input arguments the function takes arr - pointer to the beginning of the array, size - size of the array, number - number by which all array elements will be divided. The function returns a pointer to the first element of the modified array.


  • Array elements to a power

template <typename typeArr, typename typeNum>
typeArr* powArr(typeArr* arr, const int size, typeNum gpow)

As input arguments the function takes arr - pointer to the beginning of the array, size - size of the array, gpow - degree to which all elements of the array will be raised. The function returns a pointer to the first element of the modified array.


  • Array element module

template <typename typeArr>
typeArr* absArr(typeArr* arr, const int size)

As input arguments the function takes arr - pointer to the beginning of the array, size - size of the array. The function returns a pointer to the first element of the modified array.


  • Changing signs before elements in an array

template <typename typeArr>
typeArr* swapArr(typeArr* arr, const int size)

As input arguments the function takes arr - pointer to the beginning of the array, size - size of the array. The function returns a pointer to the first element of the modified array.


  • Filling an array with random elements

template <typename typeArr>
typeArr* randArr(typeArr* arr, const int size)

As input arguments the function takes arr - pointer to the beginning of the array, size - size of the array. The function returns a pointer to the first element of the modified array.


  • Combining two arrays into one large one

template <typename typeArr>
typeArr* uniArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

As input arguments the function takes arr0 and arr1 - pointers to the beginning of the arrays, arr2 - pointer to the first element of the array, which will be the result of combining two arrays, size - size of arrays (the same for the first two). The function returns a pointer to the first element of the modified array. Note: The final array is the sum of the sizes of the previous two arrays. The first two arrays must be the same size and type.


  • Combining two matrices (sum)

template <typename typeMat>
typeMat* sumMat(typeMat* mat0, typeMat* mat1, typeMat* mat2, const int isize, const int jsize)

As input arguments the function takes mat0 and mat1 - pointers to the beginning of matrices, mat2 - pointer to the first element of the matrix which will be the result of sum of elements of two matrices, isize - number of lines in matrix, jsize - number of columns in matrix. The function returns a pointer to the first element of the final matrix.


  • Combining two matrices (difference)

template <typename typeMat>
typeMat* minMat(typeMat* mat0, typeMat* mat1, typeMat* mat2, const int isize, const int jsize)

As input arguments the function takes mat0 and mat1 - pointers to the beginning of matrices, mat2 - pointer to the first element of the matrix, which will be the result of the difference of elements of two matrices, isize - number of lines in matrix, jsize - number of columns in matrix. The function returns a pointer to the first element of the resulting matrix.


  • The union of two matrices (multiplication)

template <typename typeMat>
typeMat* mulMat(typeMat* mat0, typeMat* mat1, typeMat* mat2, const int isize, const int jsize)

As input arguments the function takes mat0 and mat1 - pointers to the beginning of matrices, mat2 - pointer to the first element of the matrix which will be the result of product of elements of two matrices, isize - number of lines in matrix, jsize - number of columns in matrix. The function returns a pointer to the first element of the resulting matrix.


  • Combining two matrices (division)

template <typename typeMat>
typeMat* divMat(typeMat* mat0, typeMat* mat1, typeMat* mat2, const int isize, const int jsize)

As input arguments the function takes mat0 and mat1 - pointers to the beginning of matrices, mat2 - pointer to the first element of the matrix, which will be the result of division of elements of two matrices, isize - number of lines in matrix, jsize - number of columns in matrix. The function returns a pointer to the first element of the final matrix. Important: The function works on the principle of dividing the element of the first matrix by the element of the second matrix.


  • Adding a number to all matrix elements

template <typename typeMat, typename typeNum>
typeMat* inPlusMat(typeMat* mat, const int isize, const int jsize, typeNum number)

As input arguments the function takes mat - pointer to the beginning of the matrix, isize - number of rows in the matrix, jsize - number of columns in the matrix, number - number to add. The function returns a pointer to the first element of the resulting matrix.


  • Subtracting a number from all matrix elements

template <typename typeMat, typename typeNum>
typeMat* inMinMat(typeMat* mat, const int isize, const int jsize, typeNum number)

As input arguments the function takes mat - pointer to the beginning of the matrix, isize - number of rows in the matrix, jsize - number of columns in the matrix, number - subtracted number. The function returns a pointer to the first element of the resulting matrix.


  • Multiplying a number by all matrix elements

template <typename typeMat, typename typeNum>
typeMat* inMulMat(typeMat* mat, const int isize, const int jsize, typeNum number)

As input arguments the function takes mat - pointer to the beginning of the matrix, isize - number of rows in the matrix, jsize - number of columns in the matrix, number - number by which the matrix elements should be multiplied. The function returns a pointer to the first element of the resulting matrix.


  • Dividing all matrix elements by a number

template <typename typeMat, typename typeNum>
typeMat* inDivMat(typeMat* mat, const int isize, const int jsize, typeNum number)

As input arguments the function takes mat - pointer to the beginning of the matrix, isize - number of rows in the matrix, jsize - number of columns in the matrix, number - number by which all matrix elements will be divided. The function returns a pointer to the first element of the final matrix.


  • Expanding matrix elements

template <typename typeMat, typename typeNum>
typeMat* powMat(typeMat* mat, const int isize, const int jsize, typeNum gpow)

As input arguments the function takes mat - pointer to the beginning of the matrix, isize - number of rows in the matrix, jsize - number of columns in the matrix, gpow - degree to which all elements of the array will be raised. The function returns a pointer to the first element of the resulting matrix.


  • Module of matrix elements

template <typename typeMat>
typeMat* absMat(typeMat* mat, const int isize, const int jsize)

As input arguments the function takes mat - pointer to the beginning of the matrix, isize - number of rows in the matrix, jsize - number of columns in the matrix. The function returns a pointer to the first element of the final matrix.


  • Changing signs before numbers in the matrix

template <typename typeMat>
typeMat* swapMat(typeMat* mat, const int isize, const int jsize)

As input arguments the function takes mat - pointer to the beginning of the matrix, isize - number of rows in the matrix, jsize - number of columns in the matrix. The function returns a pointer to the first element of the final matrix.


  • Filling a matrix with random elements

template <typename typeMat>
typeMat* randMat(typeMat* mat, const int isize, const int jsize)

As input arguments the function takes mat - pointer to the beginning of the matrix, isize - number of rows in the matrix, jsize - number of columns in the matrix. The function returns a pointer to the first element of the final matrix.


🇷🇺 Русская категория

Простая арифметика

  • Проверка числа на простоту

bool isPrime(uint64_t number)

В качестве входного аргумента функция принимает число number, которое нужно проверить. Функция возвращает true - если число простое и false - если составное.


Арифметическая и геометрическая прогрессии

  • N-ый член арифметической прогрессии

long double nTermOfASequence(long double a1, long double d, uint64_t n)

В качестве входных аргументов функция принимает первый элемент прогрессии - a1, разницу - d и номер искомого элемента - n. Функция возвращает значение n-го элемента.


  • Сумма членов арифметической прогрессии

long double sumAprogression(long double a1, long double an, uint64_t n)

В качестве входных аргументов функция принимает первый элемент прогрессии - a1, значение n-го элемента - an и кол-во элементов - n. Функция возвращает сумму членов последовательности.


  • N-ый член геометрической прогрессии

long double nTermOfGSequence(long double a, long double q, uint64_t n)

В качестве входных аргументов функция принимает первый элемент прогрессии - a, знаменатель прогрессии - q и номер искомого элемента - n. Функция возвращает значение n-го элемента.


  • Сумма членов геометрической прогрессии

long double sumGprogression(long double a1, long double an, long double q)

В качестве входных аргументов функция принимает первый элемент прогрессии - a1, значение n-го элемента - an и знаменатель - q. Функция возвращает сумму членов последовательности.


Теория вероятности и комбинаторика

  • Факториал

uint64_t fac(uint64_t number)

В качестве входного аргумента функция принимает число number, которое нужно возвести в факториал. Функция возвращает факториал введенного числа.


  • Вероятность

long double prob(long double m, long double n)

В качестве входных аргументов m принимает число благоприятных исходов, n - общее число исходов испытаний. Функция возвращает вероятность события.


  • Размещение (порядок важен)

uint64_t comA(uint64_t m, uint64_t n)

Формула размещения

В качестве входных аргументов m и n, упорядоченный набор из m различных элементов из некоторого множества различных n элементов. Важно, чтобы n > m. Функция возвращает количество размещений.


  • Сочетание (порядок НЕ важен)

uint64_t comC(uint64_t m, uint64_t n)

Формула сочетания

В качестве входных аргументов m и n, набор из m элементов, выбранных из n-элементного множества, в котором не учитывается порядок элементов. Важно, чтобы n > m. Функция возвращает количество сочетаний.


  • Формула Бернулли

long double bern(uint64_t n, uint64_t k, long double p)

В качестве входных аргументов функция принимает n - общее количество испытаний, k - количество благоприятных испытаний, p - шанс благоприятного исхода. Функция возвращает вероятность заданного события.


  • Локальное число Фи

long double fiLocal(long double x)

В качестве входного аргумента функция принимает x - любое число. Функция возвращает значение локального числа Фи от заданного числа.


  • Число Фи для интегральной формулы Лапласа

long double fiIntegral(long double x)

В качестве входного аргумента функция принимает x - любое число. Функция возвращает значение числа Фи от заданного числа для интегральной формулы Лапласа.


  • Конечная часть функции для числа интегральной формулы Лапласа

 double endLaplaceTheorem(double x)

В качестве входного аргумента функция принимает x - любое число. Функция возвращает конечное число в интегральной формуле Лапласа. Комментарий: полезное практическое применение данная функция находит при расчетах в интегральной формуле Лапласа.


  • Локальная теорема Лапласа

long double lLaplace(long double n, long double k, long double p)

В качестве входных аргументов функция принимает n - общее количество испытаний, k - количество благоприятных испытаний, p - шанс благоприятного исхода. Функция возвращает вероятность заданного события.


  • Интегральная теорема Лапласа

long double iLaplace(long double k1, long double k2, long double n, long double p)

В качестве входных аргументов функция принимает k1 - количество раз, не менее которых событие наступит, k2 - количество раз, не более которых событие наступит, n - общее количество испытаний, p - шанс благоприятного исхода. Функция возвращает вероятность заданного события.


  • Дисперсия

template <typename typeArr1, typename typeArr2>
long double dispersion(typeArr1* x, typeArr2* p, const int size)

В качестве входных аргументов функция принимает x - указатель на первый элемент массива случайных величин, p - указатель на первый элемент массива вероятностей случайных величин, size - размер одного из массивов. Функция возвращает дисперсию величины. Важно! Размер обоих массивов должен быть одинаковым.


  • Стандартное отклонение дисперсии от случайной величины

template <typename typeArr1, typename typeArr2>
long double sDev(typeArr1* x, typeArr2* p, const int size)

В качестве входных аргументов функция принимает x - указатель на первый элемент массива случайных величин, p - указатель на первый элемент массива вероятностей случайных величин, size - размер одного из массивов. Функция возвращает отклонение дисперсии от случайной величины. Важно! Размер обоих массивов должен быть одинаковым.


Численные методы решения нелинейных уравнений

  • Метод бисекции(деление пополам)

template<typename F>
long double halfDivisionMethod(F func, long double a, long double b, long double e = 0.001)

В качестве входных аргументов функция принимает уравнение func, левую и правую границы отрезка a & b и необязательный параметр точности e. Функция возвращает корень уравнения на заданном промежутке, с заданной точностью.

Пример использования:

double f(double x)
{
  return (tan(0.3 * x + 0.4) - pow(x, 2));
}

int main
{
  cout << "halfDivisionMethod: " << mathAlgo::halfDivisionMethod(&f, 0, 2) << endl;
}

Вывод:

halfDivisionMethod: 0.88623

  • Метод секущих

template<typename F>
long double secantMethod(F func, long double x0, long double x1, long double e = 0.001)

В качестве входных аргументов функция принимает уравнение func, левую и правую границы отрезка x0 & x1 и необязательный параметр точности e. Функция возвращает корень уравнения на заданном промежутке, с заданной точностью.

Пример использования:

double f(double x)
{
  return (tan(0.3 * x + 0.4) - pow(x, 2));
}

int main
{
  cout << "secantMethod: " << mathAlgo::secantMethod(&f, 0, 2) << endl;
}

Вывод:

secantMethod: 0.886345

  • Метод парабол

template<typename F>
long double parabolaMethod(F func, long double a, long double b, long double e = 0.001)

В качестве входных аргументов функция принимает уравнение func, левую и правую границы отрезка a & b и необязательный параметр точности e. Функция возвращает корень уравнения на заданном промежутке, с заданной точностью.

Пример использования:

double f(double x)
{
  return (tan(0.3 * x + 0.4) - pow(x, 2));
}

int main
{
  cout << "parabolaMethod: " << mathAlgo::parabolaMethod(&f, 0, 2) << endl;
}

Вывод:

parabolaMethod: 0.886345

Рекурсивные алгоритмы

  • Число Фибоначчи

uint64_t fibonacci(uint64_t n)

В качестве входного аргумента функция принимает число n. Функция возвращает значение последовательности Фибоначчи в заданом положении.


Геометрия

  • Котангенс

long double cot(long double number)

В качестве входного аргумента функция принимает число number, котангенс которого нужно получить. Функция возвращает котангенс введенного числа.


  • Арккотангенс

long double acot(long double number)

В качестве входного аргумента функция принимает число number, арккотангенс которого нужно получить. Функция возвращает арккотангенс введенного числа.


  • Расчет длины отрезка

long double lengthOfLine(long double x1, long double x2, 
                         long double y1, long double y2, 
                         long double z1 = 0, long double z2 = 0)

В качестве входных аргументов функция принимает координаты точек A(x1, y1) & B(x2, y2)(при трехмерной системе координат вводятся координаты z). Функция возвращает длину отрезка.


Работа с массивами и матрицами

  • Поиск минимального значения в массиве

template <typename typeArr>
typeArr aMin(typeArr* arr, const int size)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива. Функция возвращает минимальный элемент массива.


  • Поиск максимального значения в массиве

template <typename typeArr>
typeArr aMax(typeArr* arr, const int size)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива. Функция возвращает максимальный элемент массива.


  • Сортировка массива методом пузырька

template <typename typeArr>
typeArr* bSort(typeArr* arr, const int size, bool asc = true)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива, аргумент asc не обязателен для заполнения, по-умолчанию true - сортировка по-возрастанию, false - по-убыванию. Функция возвращает указатель на первый элемент отсортированного массива.


  • Среднее значение массива

template<typename typeArr>
typeArr avgArr(typeArr* arr, const int size)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива. Функция возвращает среднее значение массива.


  • Мода массива

template <typename typeArr>
typeArr modenum(typeArr* arr, const int size)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива. Функция возвращает наиболее часто встречающееся число.


  • Медиана массива

template<typename typeArr>
typeArr median(typeArr* arr, const int size)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива. Функция возвращает медиану массива.


  • Суммирование двух массивов

template <typename typeArr>
typeArr* sumArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

В качестве входных аргументов функция принимает arr0 и arr1 - указатели на начало массивов, arr2 - указатель на первый элемент массива, в котором будут суммированы два предыдуших, size - размер массивов (одинаковый для троих). Функция возвращает указатель на первый элемент измененного массива.


  • Разница двух массивов

template <typename typeArr>
typeArr* minArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

В качестве входных аргументов функция принимает arr0 и arr1 - указатели на начало массивов, arr2 - указатель на первый элемент массива, в котором будет разница двух предыдущих массивов, size - размер массивов (одинаковый для троих). Важно! Разница элементов работает по принципу: элемент первого массива - элемент второго массива. Функция возвращает указатель на первый элемент измененного массива.


  • Умножение двух массивов

template <typename typeArr>
typeArr* mulArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

В качестве входных аргументов функция принимает arr0 и arr1 - указатели на начало массивов, arr2 - указатель на первый элемент массива, в котором будут умножены два предыдуших, size - размер массивов (одинаковый для троих). Функция возвращает указатель на первый элемент измененного массива.


  • Деление двух массивов

template <typename typeArr>
typeArr* divArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

В качестве входных аргументов функция принимает arr0 и arr1 - указатели на начало массивов, arr2 - указатель на первый элемент массива, в котором будет деление двух предыдущих массивов, size - размер массивов (одинаковый для троих). Функция возвращает указатель на первый элемент измененного массива. Важно! Деление элементов работает по принципу: элемент первого массива / элемент второго массива.


  • Добавление числа ко всем элементам массива

template <typename typeArr, typename typeNum>
typeArr* inPlusArr(typeArr* arr, const int size, typeNum number)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива, number - число, которое будет добавлено ко всем элементам. Функция возвращает указатель на первый элемент измененного массива.


  • Вычитание числа из всех элементов массива

template <typename typeArr, typename typeNum>
typeArr* inMinArr(typeArr* arr, const int size, typeNum number)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива, number - число, которое будет вычтено из всех элементов. Функция возвращает указатель на первый элемент измененного массива.


  • Умножение числа на все элементы массива

template <typename typeArr, typename typeNum>
typeArr* inMulArr(typeArr* arr, const int size, typeNum number)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива, number - число, которое будет умноженно на все элементы массива. Функция возвращает указатель на первый элемент измененного массива.


  • Деление всех элементов массива на число

template <typename typeArr, typename typeNum>
typeArr* inDivArr(typeArr* arr, const int size, typeNum number)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива, number - число, на которое будут поделенны все элементы массива. Функция возвращает указатель на первый элемент измененного массива.


  • Возведение элементов массива в степень

template <typename typeArr, typename typeNum>
typeArr* powArr(typeArr* arr, const int size, typeNum gpow)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива, gpow - степень, в которую будут возведены все элементы массива. Функция возвращает указатель на первый элемент измененного массива.


  • Модуль элементов массива

template <typename typeArr>
typeArr* absArr(typeArr* arr, const int size)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива. Функция возвращает указатель на первый элемент измененного массива.


  • Изменение знаков перед элементами в массиве

template <typename typeArr>
typeArr* swapArr(typeArr* arr, const int size)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива. Функция возвращает указатель на первый элемент измененного массива.


  • Заполнение массива рандомными элементами

template <typename typeArr>
typeArr* randArr(typeArr* arr, const int size)

В качестве входных аргументов функция принимает arr - указатель на начало массива, size - размер массива. Функция возвращает указатель на первый элемент измененного массива.


  • Объединение двух массивов в один большой

template <typename typeArr>
typeArr* uniArr(typeArr* arr0, typeArr* arr1, typeArr* arr2, const int size)

В качестве входных аргументов функция принимает arr0 и arr1 - указатели на начало массивов, arr2 - указатель на первый элемент массива, в котором будет результат объединения двух массивов, size - размер массивов (одинаковый для первых двух). Функция возвращает указатель на первый элемент измененного массива. Важно! Итоговый массив составляет сумму размеров двух предыдущих массивов. Первые два массива должны быть одинаковы по размеру и типу.


  • Объединение двух матриц (сумма)

template <typename typeMat>
typeMat* sumMat(typeMat* mat0, typeMat* mat1, typeMat* mat2, const int isize, const int jsize)

В качестве входных аргументов функция принимает mat0 и mat1 - указатели на начало матриц, mat2 - указатель на первый элемент матрицы, в которой будет результат суммы элементов двух матриц, isize - количество строк в матрице, jsize - количество столбцов в матрице. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Объединение двух матриц (разница)

template <typename typeMat>
typeMat* minMat(typeMat* mat0, typeMat* mat1, typeMat* mat2, const int isize, const int jsize)

В качестве входных аргументов функция принимает mat0 и mat1 - указатели на начало матриц, mat2 - указатель на первый элемент матрицы, в которой будет результат разницы элементов двух матриц, isize - количество строк в матрице, jsize - количество столбцов в матрице. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Объединение двух матриц (произведение)

template <typename typeMat>
typeMat* mulMat(typeMat* mat0, typeMat* mat1, typeMat* mat2, const int isize, const int jsize)

В качестве входных аргументов функция принимает mat0 и mat1 - указатели на начало матриц, mat2 - указатель на первый элемент матрицы, в которой будет результат произведения элементов двух матриц, isize - количество строк в матрице, jsize - количество столбцов в матрице. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Объединение двух матриц (деление)

template <typename typeMat>
typeMat* divMat(typeMat* mat0, typeMat* mat1, typeMat* mat2, const int isize, const int jsize)

В качестве входных аргументов функция принимает mat0 и mat1 - указатели на начало матриц, mat2 - указатель на первый элемент матрицы, в которой будет результат деления элементов двух матриц, isize - количество строк в матрице, jsize - количество столбцов в матрице. Функция возвращает указатель на первый элемент итоговой матрицы. ВАЖНО! Функция работает по принципу деления элемента первой матрицы на элемент второй матрицы.


  • Добавление числа ко всем элементам матрицы

template <typename typeMat, typename typeNum>
typeMat* inPlusMat(typeMat* mat, const int isize, const int jsize, typeNum number)

В качестве входных аргументов функция принимает mat - указатель на начало матрицы, isize - количество строк в матрице, jsize - количество столбцов в матрице, number - добавляемое число. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Вычитание числа из всех элементов матрицы

template <typename typeMat, typename typeNum>
typeMat* inMinMat(typeMat* mat, const int isize, const int jsize, typeNum number)

В качестве входных аргументов функция принимает mat - указатель на начало матрицы, isize - количество строк в матрице, jsize - количество столбцов в матрице, number - вычитаемое число. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Умножение числа на все элементы матрицы

template <typename typeMat, typename typeNum>
typeMat* inMulMat(typeMat* mat, const int isize, const int jsize, typeNum number)

В качестве входных аргументов функция принимает mat - указатель на начало матрицы, isize - количество строк в матрице, jsize - количество столбцов в матрице, number - число, на которое нужно умножить элементы матрицы. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Деление всех элементов матрицы на число

template <typename typeMat, typename typeNum>
typeMat* inDivMat(typeMat* mat, const int isize, const int jsize, typeNum number)

В качестве входных аргументов функция принимает mat - указатель на начало матрицы, isize - количество строк в матрице, jsize - количество столбцов в матрице, number - число, на которое будут поделены все элементы матрицы. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Возведение элементов матрицы в степень

template <typename typeMat, typename typeNum>
typeMat* powMat(typeMat* mat, const int isize, const int jsize, typeNum gpow)

В качестве входных аргументов функция принимает mat - указатель на начало матрицы, isize - количество строк в матрице, jsize - количество столбцов в матрице, gpow - степень, в которую будут возведены все элементы массива. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Модуль элементов матрицы

template <typename typeMat>
typeMat* absMat(typeMat* mat, const int isize, const int jsize)

В качестве входных аргументов функция принимает mat - указатель на начало матрицы, isize - количество строк в матрице, jsize - количество столбцов в матрице. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Смена знаков перед числами в матрице

template <typename typeMat>
typeMat* swapMat(typeMat* mat, const int isize, const int jsize)

В качестве входных аргументов функция принимает mat - указатель на начало матрицы, isize - количество строк в матрице, jsize - количество столбцов в матрице. Функция возвращает указатель на первый элемент итоговой матрицы.


  • Заполнение матрицы рандомными элементами

template <typename typeMat>
typeMat* randMat(typeMat* mat, const int isize, const int jsize)

В качестве входных аргументов функция принимает mat - указатель на начало матрицы, isize - количество строк в матрице, jsize - количество столбцов в матрице. Функция возвращает указатель на первый элемент итоговой матрицы.

Clone this wiki locally