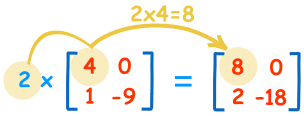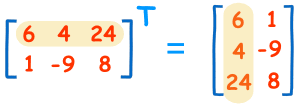In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns. For example, the dimension of the matrix below is 2 × 3 (read "two by three"), because there are two rows and three columns:
| 1 9 -13 |
| 20 5 -6 |
An m × n matrix: the m rows are horizontal, and the n columns are vertical. Each element of a matrix is often denoted by a variable with two subscripts. For example, a2,1 represents the element at the second row and first column of the matrix
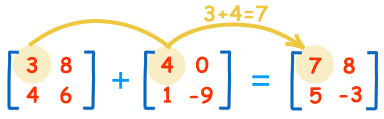
To add two matrices: add the numbers in the matching positions:
The two matrices must be the same size, i.e. the rows must match in size, and the columns must match in size.
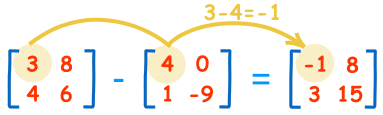
To subtract two matrices: subtract the numbers in the matching positions:
We can multiply a matrix by a constant (the value 2 in this case):
To multiply a matrix by another matrix we need to do the dot product of rows and columns.
To work out the answer for the 1st row and 1st column:
Here it is for the 1st row and 2nd column:
If we'll do the same for the rest of the rows and columns we'll get the following resulting matrix:
To "transpose" a matrix, swap the rows and columns.
We put a "T" in the top right-hand corner to mean transpose: