https://leetcode-cn.com/problems/rotate-array/
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
说明:
尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
要求使用空间复杂度为 O(1) 的 原地 算法。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/rotate-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
先用一个额外的数组将最后的 k 位保存起来,然后将前面的元素右移 k 位,再用事先保存的 k 位元素填充数组开头。
- 时间复杂度:$O(N)$。
- 空间复杂度:$O(k)$。
JavaScript Code
/**
* @param {number[]} nums
* @param {number} k
* @return {void} Do not return anything, modify nums in-place instead.
*/
var rotate = function (nums, k) {
const n = nums.length;
k %= n;
if (k === 0) return;
const reserved = nums.slice(n - k);
// 前 n-k 个元素右移 k 位
for (let i = n - k - 1; i >= 0; i--) {
nums[i + k] = nums[i];
}
// 用原本的后 k 位填充数组开头
for (let i = 0; i < reserved.length; i++) {
nums[i] = reserved[i];
}
};- 时间复杂度:$O(N)$。
- 空间复杂度:$O(1)$。
JavaScript Code
/**
* @param {number[]} nums
* @param {number} k
* @return {void} Do not return anything, modify nums in-place instead.
*/
var rotate = function (nums, k) {
const n = nums.length;
k %= n;
if (k === 0) return;
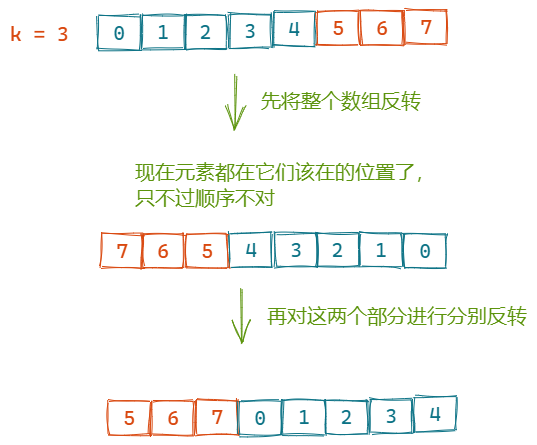
reverse(nums, 0, n - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, n - 1);
// ********************************
// 反转某一段数组
function reverse(arr, l, r) {
while (l < r) {
[arr[l], arr[r]] = [arr[r], arr[l]];
l++;
r--;
}
}
};代码中 count 的来源可以去看官方题解的证明。
- 时间复杂度:$O(N)$。
- 空间复杂度:$O(1)$。
JavaScript Code
/**
* @param {number[]} nums
* @param {number} k
* @return {void} Do not return anything, modify nums in-place instead.
*/
var rotate = function (nums, k) {
const n = nums.length;
k %= n;
const count = gcd(k, n);
for (let start = 0; start < count; start++) {
let p = start;
let prev = nums[p];
// 从 start 开始跳,再跳回到 start 的时候停止
// 由于此时不一定遍历到了所有元素,所以 start++ 后再重复步骤
do {
const next = (p + k) % n;
[prev, nums[next]] = [nums[next], prev];
p = next;
} while (p !== start);
}
// *********************************
// 最大公约数
function gcd(x, y) {
return y ? gcd(y, x % y) : x;
}
};