Source code can be found here. Documentation can be found here.
To the documentation page for pymead, a Python GUI and API for generation, aerodynamic analysis, and shape optimization of parametric airfoil systems. This parametrization framework in its preliminary stage was presented at the 2022 AIAA Aviation Conference in Chicago, IL under the title "A Parametrization Framework for Multi-Element Airfoil Systems Using Bézier Curves."
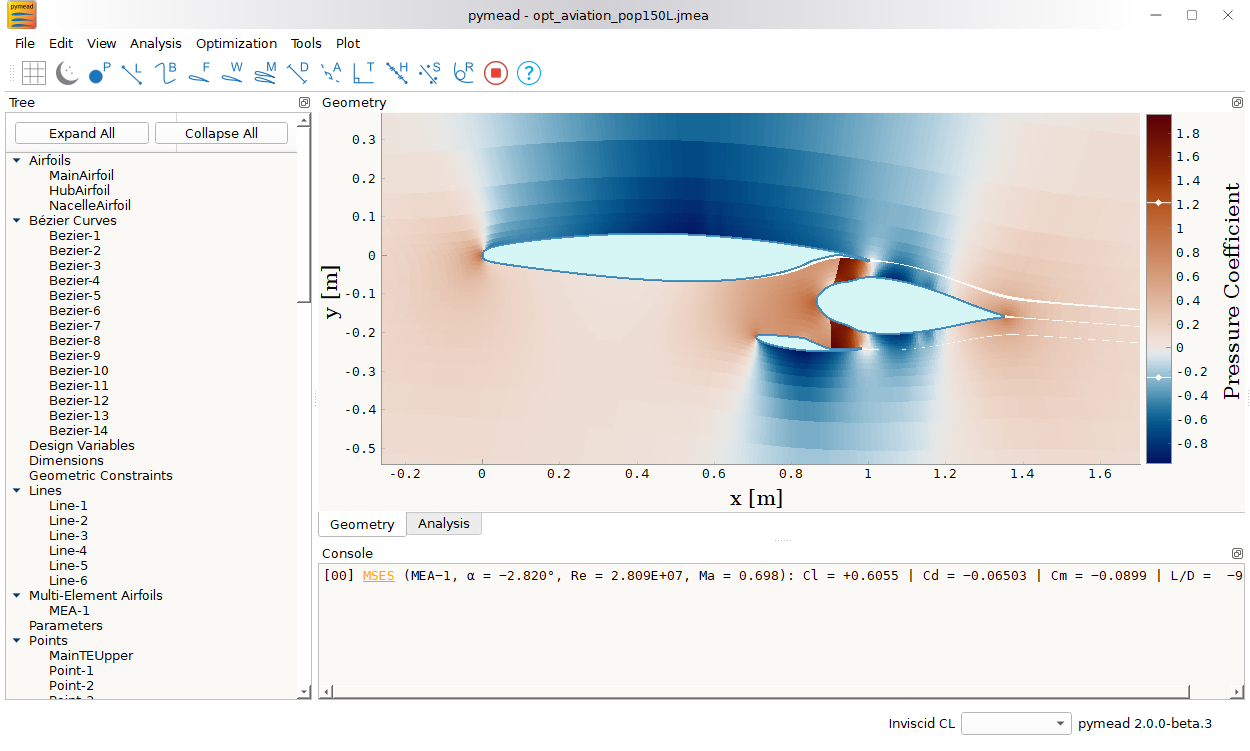
The creation of this package was motivated by a research aircraft application: the aerodynamic design of a propulsion-airframe-integrated commercial transport aircraft. The cross-section of a wing or fuselage with integrated propulsors can be represented, with some sacrifice in fidelity, as a quasi-2D multi-element airfoil system. This multi-element airfoil system comprises a main airfoil (either the fuselage or main airfoil element), a hub airfoil (representing the cross-section of an axisymmetric hub), and a nacelle airfoil (representing the cross-section of an axisymmetric nacelle).
For access to both the API and GUI, pymead can be installed using the typical pip install pymead.
There are several other installation options, including a standalone Windows installer.
See the pymead installation page for more details.
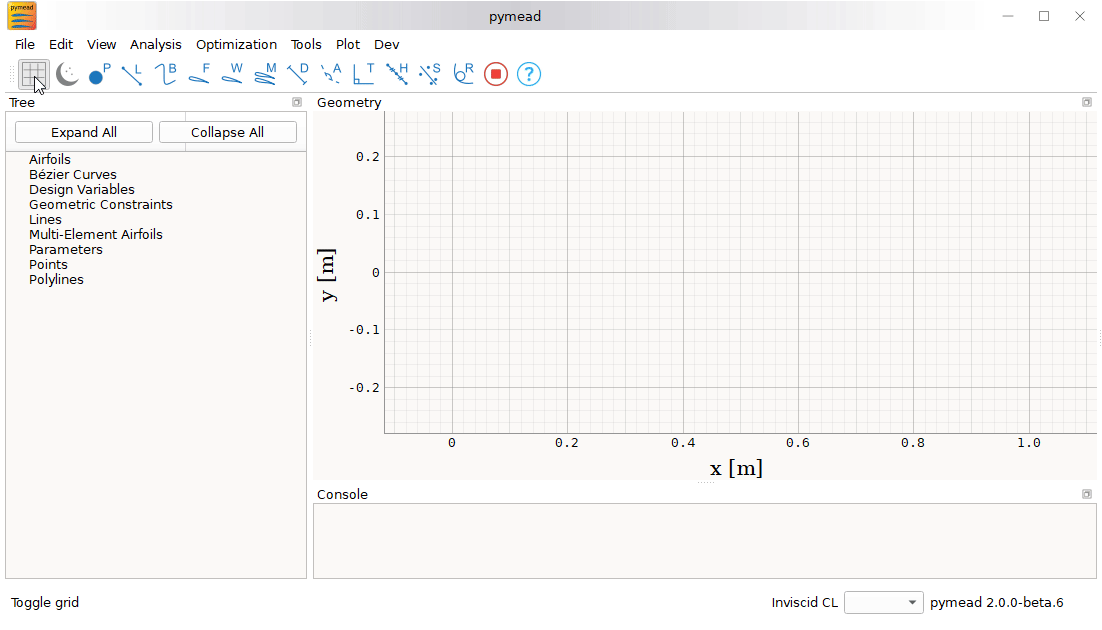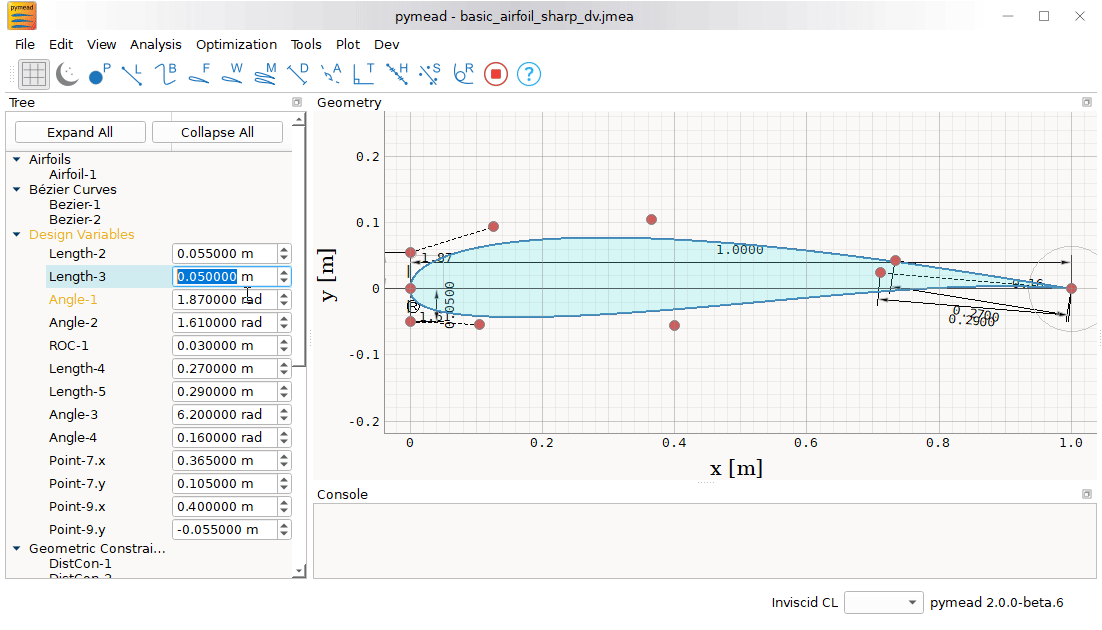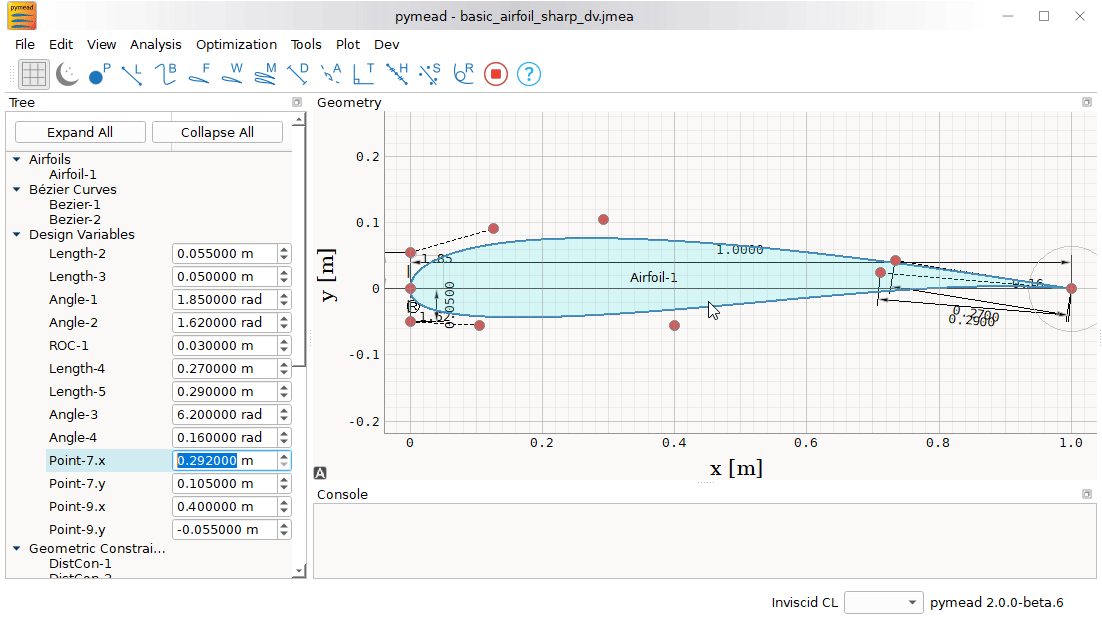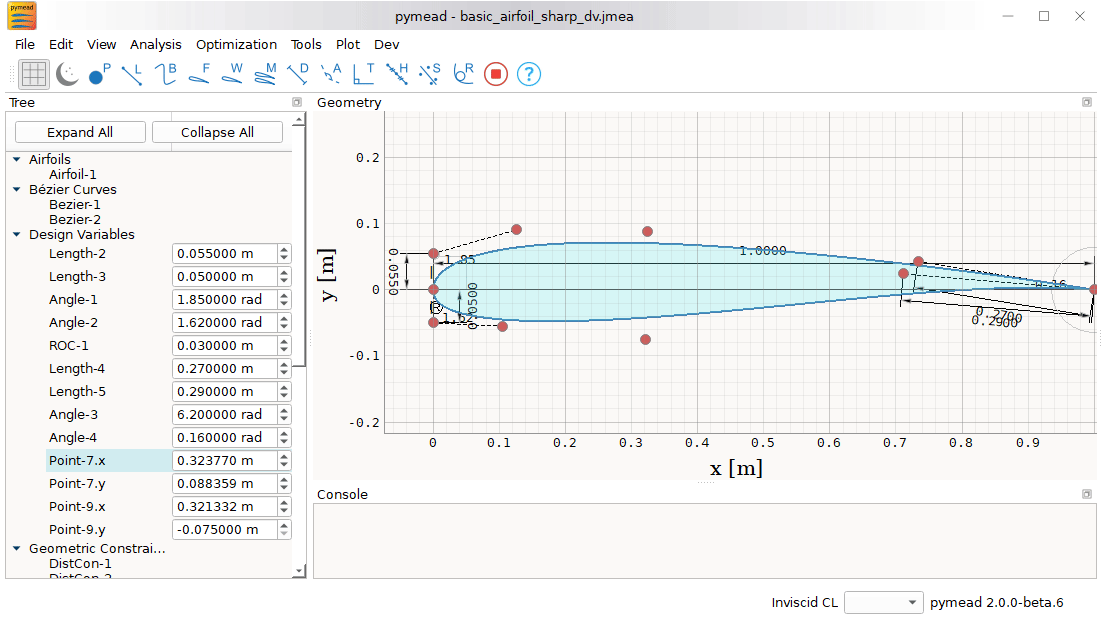
By using a well-defined parametrization framework, this airfoil system can be morphed or deformed in a variety of ways
using changes in high-level design variables. These design variables are represented by
pymead.core.param.DesVar objects in this framework, which have modifiable lower and upper bounds for optimization.
This facilitates aerodynamic analysis, parametric sweeps, and even shape optimization.
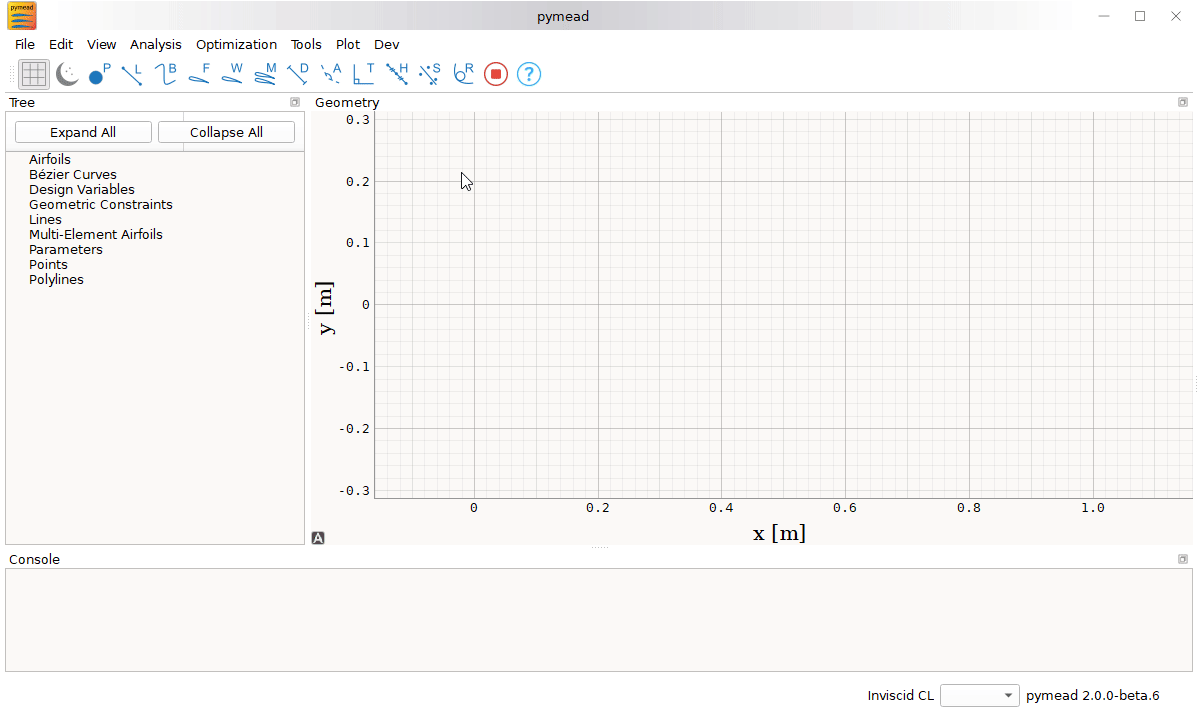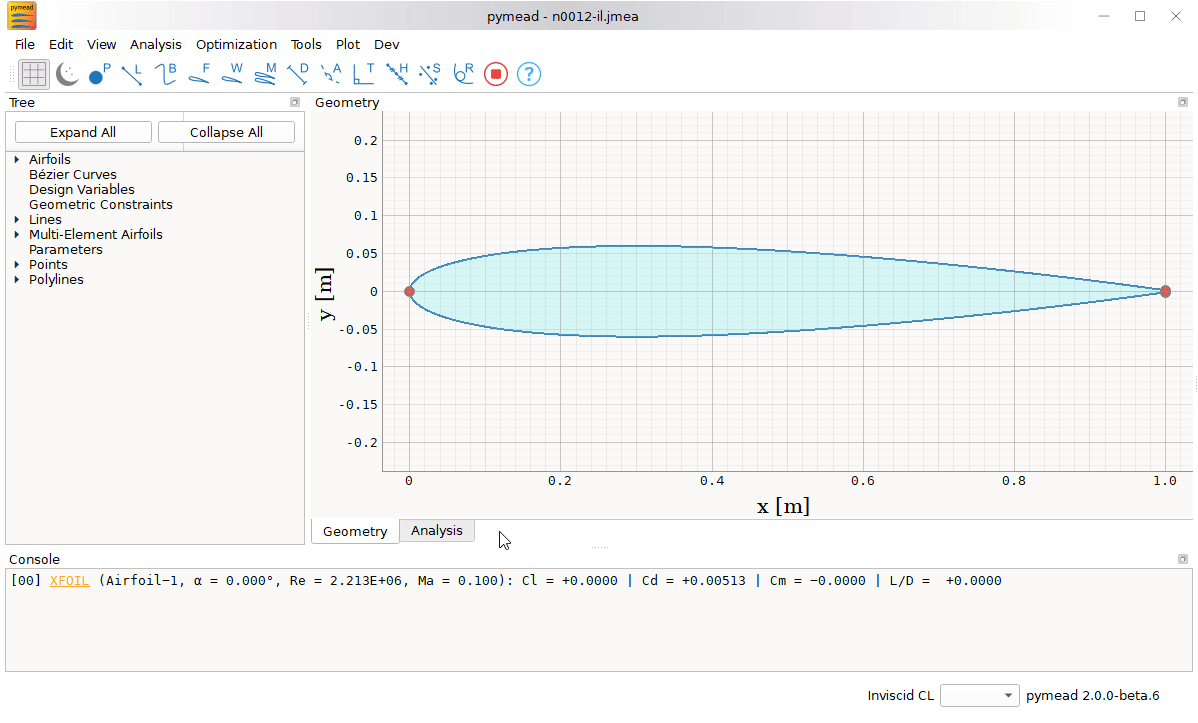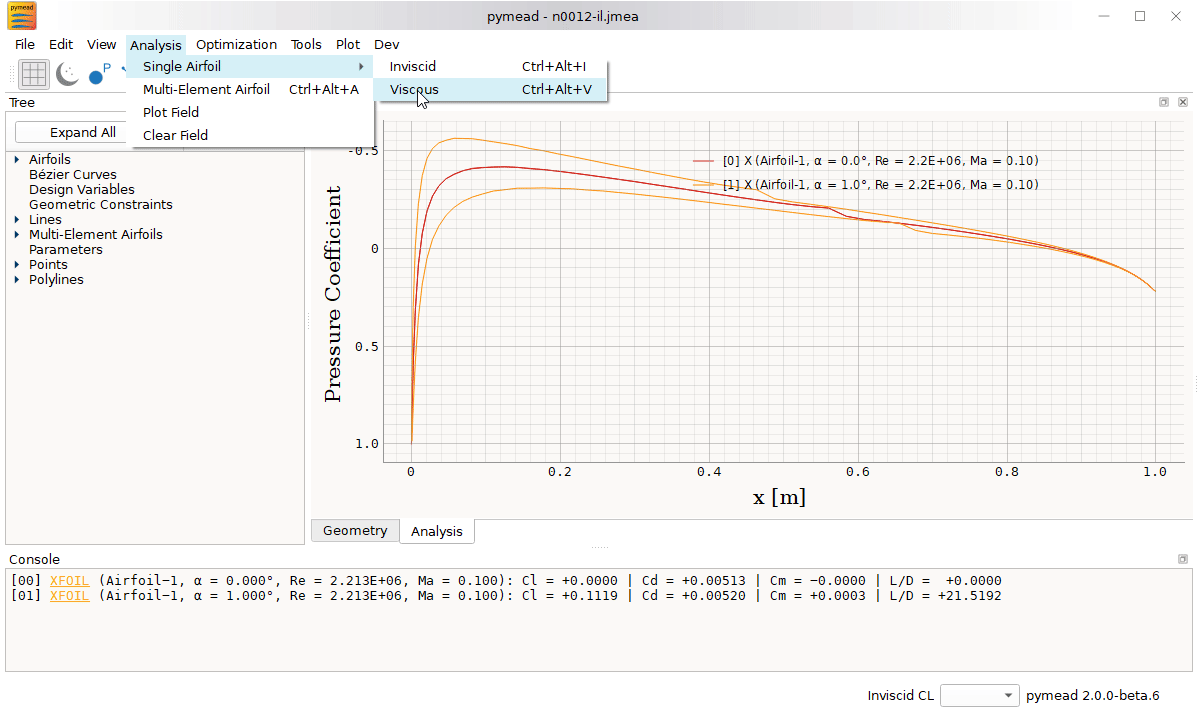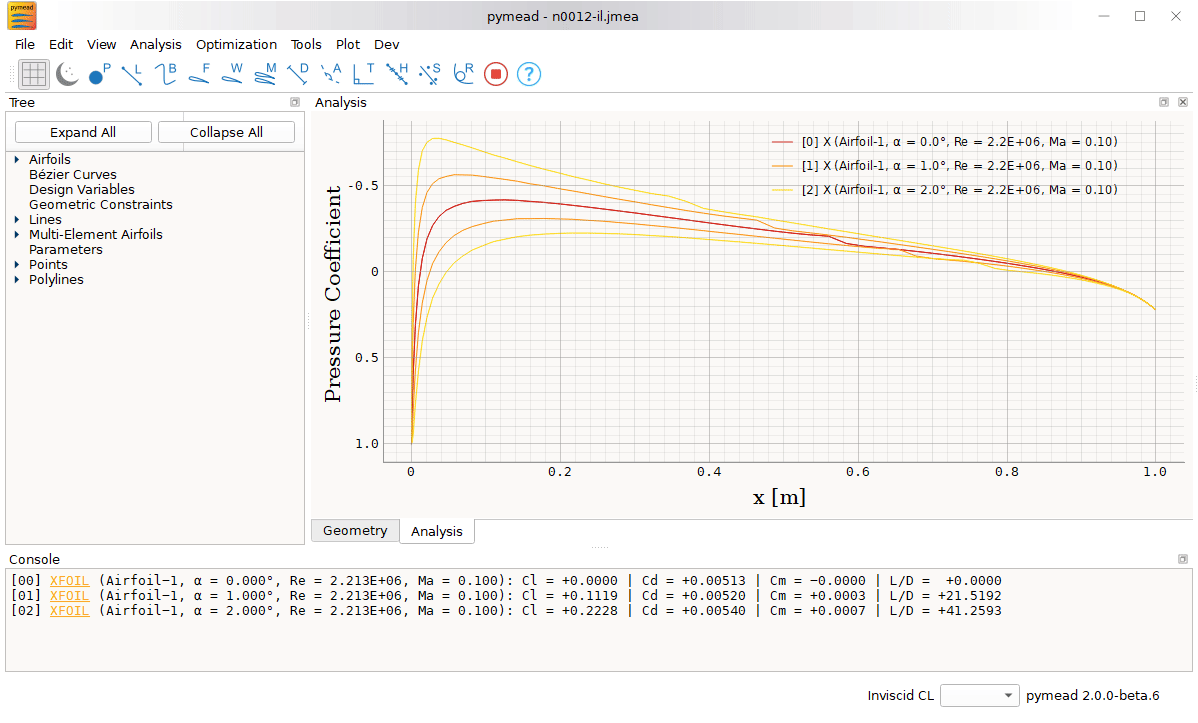
pymead has both an application programming interface (API) and a graphical user interface (GUI), either of which can be used to define airfoil geometries from basic geometries (like points, lines, and curves), implement geometric constraints, perform analysis using wrappers for XFOIL and MSES, match existing airfoils with Bézier curves, and even execute aerodynamic or aeropropulsive shape optimization studies. See the documentation site under development for GUI tutorials and API tutorials.
It is the hope of the author that pymead is sufficiently flexible to be used for airfoil applications of varying complexities, from simple, single-airfoil design to high-fidelity, multi-element airfoil shape optimization. Other common multi-element airfoil systems, such as the high-lift configuration on an aircraft, are also target applications for this software package.
One utility provided in this software package which may be useful in the start-up phase of airfoil design is
pymead.optimization.airfoil_matching.match_airfoil(). This function allows the matching of a particular
parametrization to any public airfoil geometry at airfoiltools.com using the gradient-based "SLSQP"
optimizer. See the pymead gallery for more example
applications.
This work was supported by NASA under award number 80NSSC19M0125 as part of the Center for High-Efficiency Electrical Technologies for Aircraft (CHEETA).
Author: Matthew G Lauer
Email: [email protected]
- Version notes have migrated to pymead's GitHub releases page
- Corrections to README.md for PyPi long project description (images not showing properly)
- Made corrections on BaseAirfoilParams and AnchorPoint Args domains
- Added support for zero-curvature anchor points using 180-degree curvature control arm angles (or 90-degree curvature control arm angles for the leading edge)
- Added support for sharp-juncture anchor points with R=0 or R_{LE}=0. Adding multiple consecutive sharp juncture anchor points creates line segments. Adding sharp-juncture anchor points violates the principle of slope and curvature continuity, but may be useful in some cases.