On February 1st 2016, a security advisory was posted to Openwall by a Socat developer: Socat security advisory 7 - Created new 2048bit DH modulus
In the OpenSSL address implementation the hard coded 1024 bit DH p parameter was not prime. The effective cryptographic strength of a key exchange using these parameters was weaker than the one one could get by using a prime p. Moreover, since there is no indication of how these parameters were chosen, the existence of a trapdoor that makes possible for an eavesdropper to recover the shared secret from a key exchange that uses them cannot be ruled out.
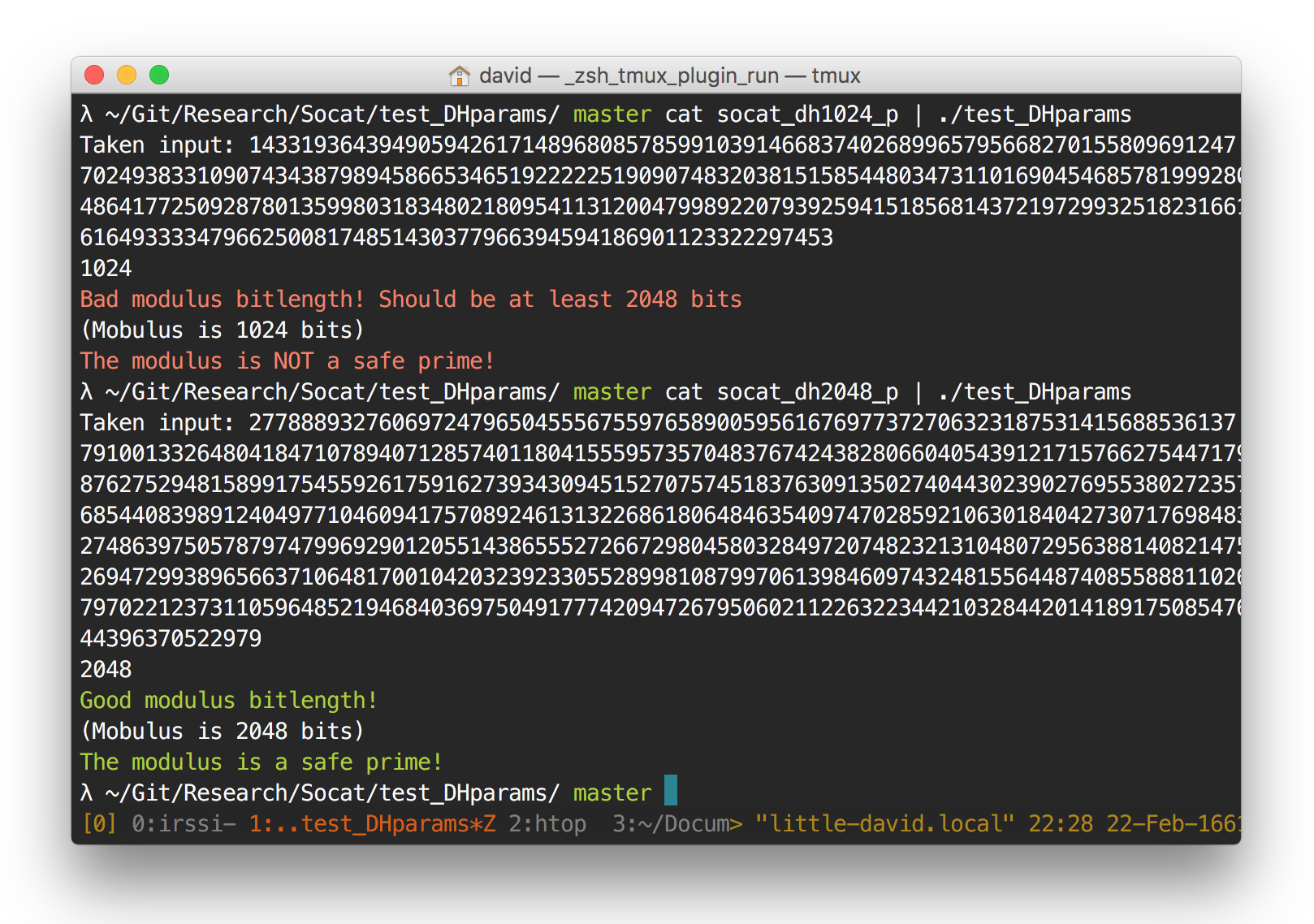
A new prime modulus p parameter has been generated by Socat developer using OpenSSL dhparam command.
In addition the new parameter is 2048 bit long.
This is a pretty weird message with a Juniper feeling to it.
Socat's README tells us that you can use their free software to setup an encrypted tunnel for data transfer between two peers.
Looking at the commit logs you can see that they used a 512 bits Diffie-Hellman modulus until last year (2015) January when it was replaced with a 1024 bits one.
Socat did not work in FIPS mode because 1024 instead of 512 bit DH prime is required. Thanks to Zhigang Wang for reporting and sending a patch.
The person who pushed the commit is Gerhard Rieger who is the same person who fixed it a year later. In the comment he refers to an Oracle employee at the time who has yet to comment on his mistake. It also seems like his github account and his personal websites were deleted the day this security advisory was published.
This research's goal is to understand how this could possibly be a backdoor. And more particularly, a Nobody-but-us one (NOBUS). Here are the objectives of this research:
- Build a proof of concept of such a NOBUS backdoor
- check if we can reverse the socat backdoor to use it ourselves
- Try to answer the question: "does it look like a backdoor?"
Before shouting from the rooftops the words "backdoor", let's take a step back and imagine what could have gone wrong. First, it is possible that (back then an Oracle employee) had no idea that the DH modulus should be a prime. In fact, Diffie-Hellman works well enough with composite modulus (but keep in mind that it has its share of problems, and we will see later why). Also, what if he did generated a prime but got lost afterwards?
(The employee also closed his github account and personal website the day the advisory was published).
Throughout TLS, and in Socat's case throughout OpenSSL, the use of big endianness is enforced for long numbers formatting. That is: you read a byte string from left to right to convert it to a number. This can make the process of converting from and to numbers a confusing task.
static unsigned char dh1024_p[] = {
0xCC, 0x17, 0xF2, 0xDC, 0x96, 0xDF, 0x59, 0xA4, 0x46, 0xC5, 0x3E, 0x0E,
0xB8, 0x26, 0x55, 0x0C, 0xE3, 0x88, 0xC1, 0xCE, 0xA7, 0xBC, 0xB3, 0xBF,
0x16, 0x94, 0xD8, 0xA9, 0x45, 0xA2, 0xCE, 0xA9, 0x5B, 0x22, 0x25, 0x5F,
0x92, 0x59, 0x94, 0x1C, 0x22, 0xBF, 0xCB, 0xC8, 0xC8, 0x57, 0xCB, 0xBF,
0xBC, 0x0E, 0xE8, 0x40, 0xF9, 0x87, 0x03, 0xBF, 0x60, 0x9B, 0x08, 0xC6,
0x8E, 0x99, 0xC6, 0x05, 0xFC, 0x00, 0xD6, 0x6D, 0x90, 0xA8, 0xF5, 0xF8,
0xD3, 0x8D, 0x43, 0xC8, 0x8F, 0x7A, 0xBD, 0xBB, 0x28, 0xAC, 0x04, 0x69,
0x4A, 0x0B, 0x86, 0x73, 0x37, 0xF0, 0x6D, 0x4F, 0x04, 0xF6, 0xF5, 0xAF,
0xBF, 0xAB, 0x8E, 0xCE, 0x75, 0x53, 0x4D, 0x7F, 0x7D, 0x17, 0x78, 0x0E,
0x12, 0x46, 0x4A, 0xAF, 0x95, 0x99, 0xEF, 0xBC, 0xA6, 0xC5, 0x41, 0x77,
0x43, 0x7A, 0xB9, 0xEC, 0x8E, 0x07, 0x3C, 0x6D,
};Update from Samuel Nieves, "interpreting the modulus bytes as 16-bit words in little-endian order does get us a prime":
3c6d8e07b9ec437a4177a6c5efbc95994aaf1246780e7d17
4d7f75538ecebfabf5af04f66d4f37f086734a0b046928ac
bdbb8f7a43c8d38df5f890a8d66dfc00c6058e9908c6609b
03bff987e840bc0ecbbfc857cbc822bf941c9259255f5b22
cea945a2d8a91694b3bfa7bcc1cee388550cb8263e0e46c5
59a496dff2dccc17
This is indeed a prime! But not a safe prime!
It might comes as a shock to the non-enlightened, but we usually do not take the time to generate real primes, or what we more generally call provable primes. Efficient provable tests like ECPP or AKS do exists, but the accuracy and the speed of probable tests (tests that either tell you if a number is probably a prime, or definitely not a prime) are good enough that any margin of error is negligible.
Examples of probable tests are given in appendix C.3 of the . Most implementations will use the \emph{Miller-Rabin} test with a variable amount of iteration according to the degree of certainty they want to achieve.
For example in , the number of iteration is chosen such that the risk of yielding a false positive (a non-prime prime) is of at most
1/2^{80}. To understand what this means in practice: it is as likely to happen as being hit by a meteorite while winning the Powerball. Here's a quote from the Structure and Interpretation of Computer Programs book:
Numbers that fool the Fermat test are called Carmichael numbers, and little is known about them other than that they are extremely rare. There are 255 Carmichael numbers below 100,000,000. The smallest few are 561, 1105, 1729, 2465, 2821, and 6601. In testing primality of very large numbers chosen at random, the chance of stumbling upon a value that fools the Fermat test is less than the chance that cosmic radiation cosmic radiation will cause the computer to make an error in carrying out a "correct" algorithm. Considering an algorithm to be inadequate for the first reason but not for the second illustrates the difference between mathematics and engineering.
There are ways to maliciously generate such fake primes, here's a paper on it, but this only works on the deterministic version of the Rabin Miller test. To test Rabin Miller you can take random bases OR you can always run it with the same set of bases (which is the deterministic version of the test). They show that you can choose a number n = p * q, where p and q are somehow related and they will pass the test for every base b if b is coprime to p and b is a square modulo q. As I said this method works if you know in advance the bases that will be used (which is rarely the case I suppose). Also it seems like you are really limited in the number of witness you fool, but this is an old paper and we might be able to do better now.
Trial division (testing every small primes up to a certain limit) has already found two small factors: 271 and 13,597. The last factor is still a composite of 1002 bits (302 digits) that we'll call C302 (C for Composite).
I tested if the generator (2) has order 271-1 or 13,597-1 or (271-1)*(13,597-1). But no.
Pollard's p-1 factorization algorithm should work fine for finding factors p if p-1 is smooth.
The records people have reached with this algorithm is to factor a ~200bits composite which largest factor was a 50bits and other factors under 30bits (with B1=10^10 and B2 =10^15).
But an attacker could have easily chosen factors of p-1 and q-1 to be of size > 50bits which would have canceled any possibility of Pollard's p-1 to factor p or q. He could have also added two 60 bits factors to void the B2 bound as well.
Another very good algorithm at factoring is the Elliptic Curve Method or ECM, that only depends on the size of the smallest factor.
The records found factors of size 276bits. This is again a problem if the backdoored modulus is composed of two 512bits primes.
The Quadratic Sieve, or QS algorithm running-time depends on the modulus's size, best for numbers under 400-500bits, and so is out of reach for our big 1024bits modulus.
Then, at some predetermined point where ECM is less likely to find a factor over time than the time taken to run a sieve method, you switch from ECM to the sieve method, which is SIQS below ~100 digits and NFS above 100 digits. These sieve methods are different in that they take a fixed amount of time for a given input number, and are guaranteed* to produce a factorization at the end. (Dubslow)
Finally the General Number Field Sieve, or the GNFS algorithm, which works according to the size of the entire modulus and not its factors, has a record of factoring 768bits in 2009. That might be our best bet, although the modulus is still too big for us to try. In the Logjam paper last year could be read that the NSA might have the capacity to do it.
Q: What are the chances that if this was non-prime was a mistake, it generated factors large enough so that no one can reverse it?
A: From Handbook of Applied Cryptography fact 3.7:
Let n be chosen uniformly at random form the interval [1, x]
- if 1/2 <= a <= 1, then the probability that the largest prime factor of n is <= x^a is approximately 1+ ln(a). Thus, for example, the probability than n has a prime factor > sqrt(x) is ln(2) ~= 0.69
- The probability that the second-largest prime factor of n is <= x^{0.2117} is about 1/2
- The expected total number of prime factors of n is ln ln x + O(1). (If n = mult(p_i^{e_i}), the total number of prime factors of n is sum(e_i).)
This means three things:
- item socat's 1024 bit composite modulus
nprobability to have a prime factor greater than 512 bits is ~0.69. - the probability that the second-largest prime factor of
nis smaller than 217 bits is 1/2. - The total number of prime factor of
nis expected to be 7 (we already have 2).
217 bits is feasible to find with ECM (maybe with p-1 factorization algorithm)
The composite prime is 1024bits long, which is too much to try factorization algorithms like QS and GNFS that depend on the number's size.
Instead I tried factoring it with both ECM and Pollard's p-1. The latter is used because it is likely that one of the factor p of the order has a 'small' factorization of p-1.
If the backdoor was done properly, or if the number was uniformly generated. It's possible that we won't find anything using this methods.
But first, trial divisions gave us 2 numbers: 271 and 13,597. The remaining factor is still a composite of 1002 bits (302 digits) that we'll call C302 (C for Composite).
a run with B1 = 1000000000 and automatic B2 didn't find anything after ~52 hours
$ ecm 1000000000 < socat_1024dh_p
GMP-ECM 6.4.4 [configured with GMP 6.0.0, --enable-asm-redc] [ECM]
Input number is 38894884397634366007356454548332370646972724268802781973440208895542936165564656473524541403310393405820598366261673173802130771236325314878371830363723788045821711985461441675679316058246609104355161134470046705337593170498462616195650378975298117141144096886684800236261920005248055422089305813639519 (302 digits)
Using B1=1000000000, B2=19071176724616, polynomial Dickson(30), sigma=943042405
Step 1 took 10019112ms
Step 2 took 1429277msA saved run of ECM ecm -pm1 1e10 1e15 that lasted 10 days can be found here: saved_ecm_run
I didn't save the previous run, although it found nothing. currently running with B1 = 10^12 which might be way too big. Will post the seed once done.
$ ecm -save socat_ecm_progress -pm1 1e12 1e15 < socat_1024dh_q
GMP-ECM 6.4.4 [configured with GMP 6.0.0, --enable-asm-redc] [P-1]
Input number is 38894884397634366007356454548332370646972724268802781973440208895542936165564656473524541403310393405820598366261673173802130771236325314878371830363723788045821711985461441675679316058246609104355161134470046705337593170498462616195650378975298117141144096886684800236261920005248055422089305813639519 (302 digits)
Using B1=1000000000000, B2=1324293386181580, polynomial x^1, x0=785660251A new order has been generated, but we know nothing about its order: checking it with test_DHparams we confirm that it is a safe prime (2q + 1) so its order is implicit (2q).