给你一个 n 个点的带权无向连通图,节点编号为 0 到 n-1 ,同时还有一个数组 edges ,其中 edges[i] = [fromi, toi, weighti] 表示在 fromi 和 toi 节点之间有一条带权无向边。最小生成树 (MST) 是给定图中边的一个子集,它连接了所有节点且没有环,而且这些边的权值和最小。
请你找到给定图中最小生成树的所有关键边和伪关键边。如果从图中删去某条边,会导致最小生成树的权值和增加,那么我们就说它是一条关键边。伪关键边则是可能会出现在某些最小生成树中但不会出现在所有最小生成树中的边。
请注意,你可以分别以任意顺序返回关键边的下标和伪关键边的下标。
示例 1:
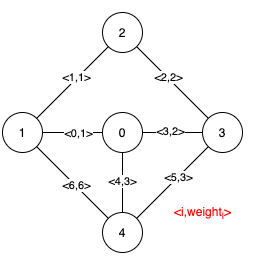
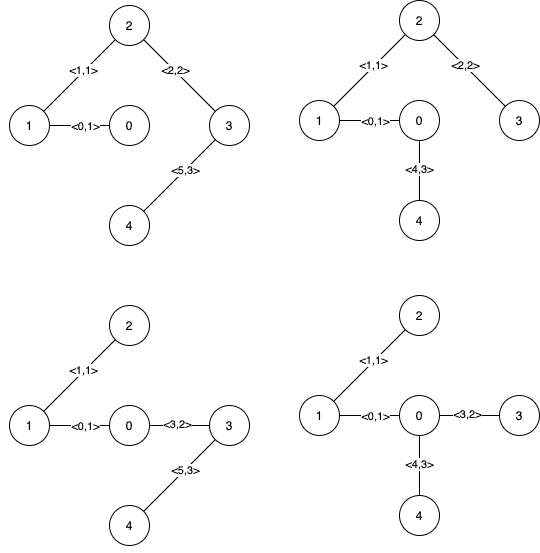
输入:n = 5, edges = [[0,1,1],[1,2,1],[2,3,2],[0,3,2],[0,4,3],[3,4,3],[1,4,6]] 输出:[[0,1],[2,3,4,5]] 解释:上图描述了给定图。 下图是所有的最小生成树。注意到第 0 条边和第 1 条边出现在了所有最小生成树中,所以它们是关键边,我们将这两个下标作为输出的第一个列表。 边 2,3,4 和 5 是所有 MST 的剩余边,所以它们是伪关键边。我们将它们作为输出的第二个列表。
示例 2 :
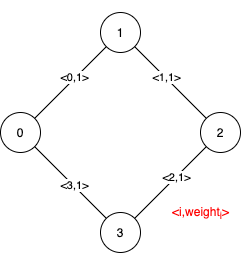
输入:n = 4, edges = [[0,1,1],[1,2,1],[2,3,1],[0,3,1]] 输出:[[],[0,1,2,3]] 解释:可以观察到 4 条边都有相同的权值,任选它们中的 3 条可以形成一棵 MST 。所以 4 条边都是伪关键边。
提示:
2 <= n <= 1001 <= edges.length <= min(200, n * (n - 1) / 2)edges[i].length == 30 <= fromi < toi < n1 <= weighti <= 1000- 所有
(fromi, toi)数对都是互不相同的。
最小生成树问题。
- 关键边:若删去某条边,导致整个图不连通,或者最小生成树的权值变大,那么这条边就是关键边。
- 伪关键边:对于非关键边,我们尝试将该边加入最小生成树集合中,若最小生成树的权值不变,那么这条边就是非关键边。
方法一:Kruskal 算法
先利用 Kruskal 算法,得出最小生成树的权值 v。然后依次枚举每条边,按上面的方法,判断是否是关键边;如果不是关键边,再判断是否是伪关键边。
class UnionFind:
def __init__(self, n):
self.p = list(range(n))
self.n = n
def union(self, a, b):
if self.find(a) == self.find(b):
return False
self.p[self.find(a)] = self.find(b)
self.n -= 1
return True
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
class Solution:
def findCriticalAndPseudoCriticalEdges(
self, n: int, edges: List[List[int]]
) -> List[List[int]]:
for i, e in enumerate(edges):
e.append(i)
edges.sort(key=lambda x: x[2])
uf = UnionFind(n)
v = sum(w for f, t, w, _ in edges if uf.union(f, t))
ans = [[], []]
for f, t, w, i in edges:
uf = UnionFind(n)
k = sum(z for x, y, z, j in edges if j != i and uf.union(x, y))
if uf.n > 1 or (uf.n == 1 and k > v):
ans[0].append(i)
continue
uf = UnionFind(n)
uf.union(f, t)
k = w + sum(z for x, y, z, j in edges if j != i and uf.union(x, y))
if k == v:
ans[1].append(i)
return ansclass Solution {
public List<List<Integer>> findCriticalAndPseudoCriticalEdges(int n, int[][] edges) {
for (int i = 0; i < edges.length; ++i) {
int[] e = edges[i];
int[] t = new int[4];
System.arraycopy(e, 0, t, 0, 3);
t[3] = i;
edges[i] = t;
}
Arrays.sort(edges, Comparator.comparingInt(a -> a[2]));
int v = 0;
UnionFind uf = new UnionFind(n);
for (int[] e : edges) {
int f = e[0], t = e[1], w = e[2];
if (uf.union(f, t)) {
v += w;
}
}
List<List<Integer>> ans = new ArrayList<>();
for (int i = 0; i < 2; ++i) {
ans.add(new ArrayList<>());
}
for (int[] e : edges) {
int f = e[0], t = e[1], w = e[2], i = e[3];
uf = new UnionFind(n);
int k = 0;
for (int[] ne : edges) {
int x = ne[0], y = ne[1], z = ne[2], j = ne[3];
if (j != i && uf.union(x, y)) {
k += z;
}
}
if (uf.getN() > 1 || (uf.getN() == 1 && k > v)) {
ans.get(0).add(i);
continue;
}
uf = new UnionFind(n);
uf.union(f, t);
k = w;
for (int[] ne : edges) {
int x = ne[0], y = ne[1], z = ne[2], j = ne[3];
if (j != i && uf.union(x, y)) {
k += z;
}
}
if (k == v) {
ans.get(1).add(i);
}
}
return ans;
}
}
class UnionFind {
private int[] p;
private int n;
public UnionFind(int n) {
p = new int[n];
this.n = n;
for (int i = 0; i < n; ++i) {
p[i] = i;
}
}
public int getN() {
return n;
}
public boolean union(int a, int b) {
if (find(a) == find(b)) {
return false;
}
p[find(a)] = find(b);
--n;
return true;
}
public int find(int x) {
if (p[x] != x) {
p[x] = find(p[x]);
}
return p[x];
}
}class UnionFind {
public:
vector<int> p;
int n;
UnionFind(int _n)
: n(_n)
, p(_n) {
iota(p.begin(), p.end(), 0);
}
bool unite(int a, int b) {
if (find(a) == find(b)) return false;
p[find(a)] = find(b);
--n;
return true;
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
};
class Solution {
public:
vector<vector<int>> findCriticalAndPseudoCriticalEdges(int n, vector<vector<int>>& edges) {
for (int i = 0; i < edges.size(); ++i) edges[i].push_back(i);
sort(edges.begin(), edges.end(), [](auto& a, auto& b) { return a[2] < b[2]; });
int v = 0;
UnionFind uf(n);
for (auto& e : edges) {
int f = e[0], t = e[1], w = e[2];
if (uf.unite(f, t)) v += w;
}
vector<vector<int>> ans(2);
for (auto& e : edges) {
int f = e[0], t = e[1], w = e[2], i = e[3];
UnionFind ufa(n);
int k = 0;
for (auto& ne : edges) {
int x = ne[0], y = ne[1], z = ne[2], j = ne[3];
if (j != i && ufa.unite(x, y)) k += z;
}
if (ufa.n > 1 || (ufa.n == 1 && k > v)) {
ans[0].push_back(i);
continue;
}
UnionFind ufb(n);
ufb.unite(f, t);
k = w;
for (auto& ne : edges) {
int x = ne[0], y = ne[1], z = ne[2], j = ne[3];
if (j != i && ufb.unite(x, y)) k += z;
}
if (k == v) ans[1].push_back(i);
}
return ans;
}
};type unionFind struct {
p []int
n int
}
func newUnionFind(n int) *unionFind {
p := make([]int, n)
for i := range p {
p[i] = i
}
return &unionFind{p, n}
}
func (uf *unionFind) find(x int) int {
if uf.p[x] != x {
uf.p[x] = uf.find(uf.p[x])
}
return uf.p[x]
}
func (uf *unionFind) union(a, b int) bool {
if uf.find(a) == uf.find(b) {
return false
}
uf.p[uf.find(a)] = uf.find(b)
uf.n--
return true
}
func findCriticalAndPseudoCriticalEdges(n int, edges [][]int) [][]int {
for i := range edges {
edges[i] = append(edges[i], i)
}
sort.Slice(edges, func(i, j int) bool {
return edges[i][2] < edges[j][2]
})
v := 0
uf := newUnionFind(n)
for _, e := range edges {
f, t, w := e[0], e[1], e[2]
if uf.union(f, t) {
v += w
}
}
ans := make([][]int, 2)
for _, e := range edges {
f, t, w, i := e[0], e[1], e[2], e[3]
uf = newUnionFind(n)
k := 0
for _, ne := range edges {
x, y, z, j := ne[0], ne[1], ne[2], ne[3]
if j != i && uf.union(x, y) {
k += z
}
}
if uf.n > 1 || (uf.n == 1 && k > v) {
ans[0] = append(ans[0], i)
continue
}
uf = newUnionFind(n)
uf.union(f, t)
k = w
for _, ne := range edges {
x, y, z, j := ne[0], ne[1], ne[2], ne[3]
if j != i && uf.union(x, y) {
k += z
}
}
if k == v {
ans[1] = append(ans[1], i)
}
}
return ans
}