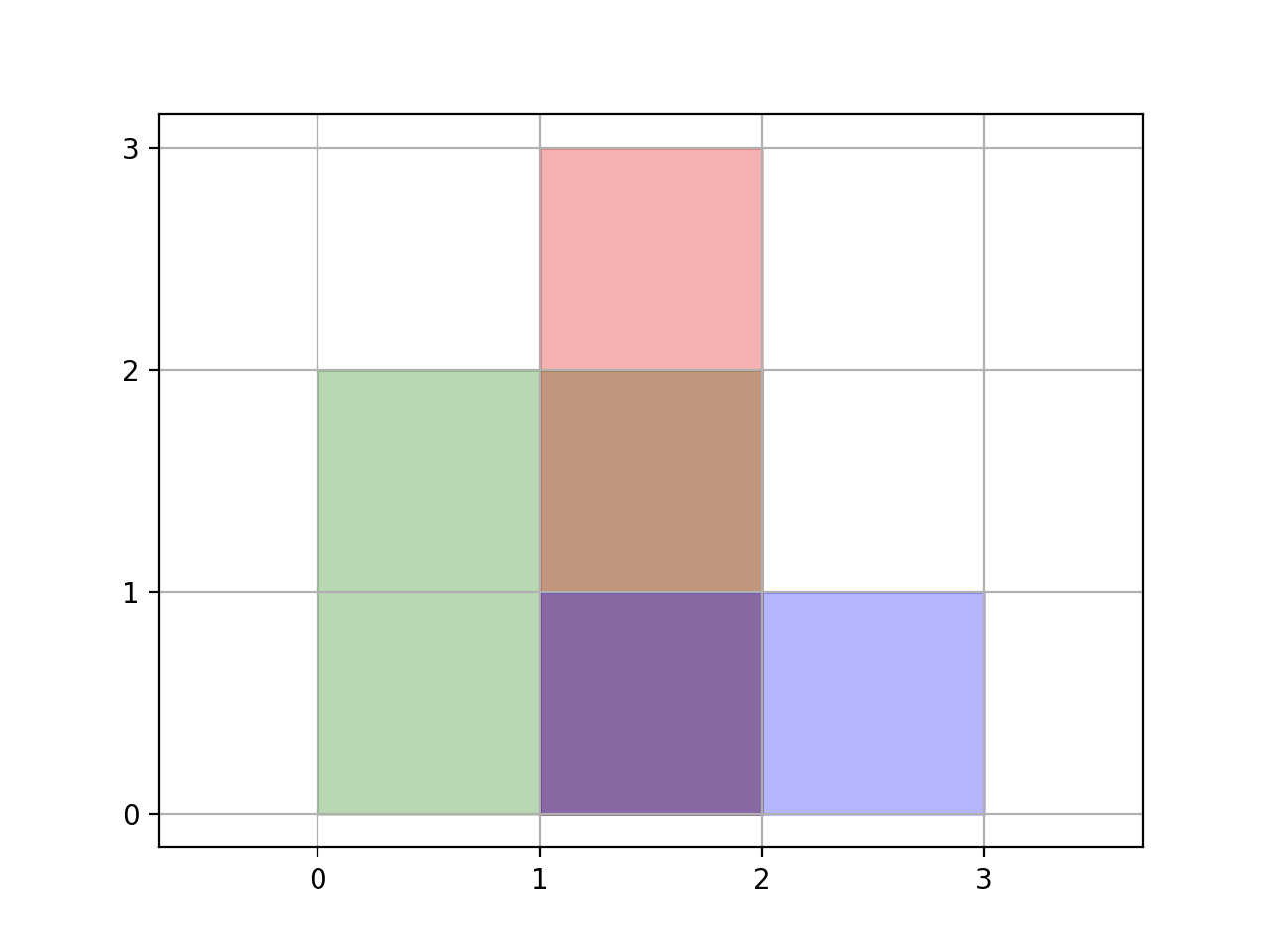Skip to content

Latest commit

 

History

History
443 lines (372 loc) · 12.1 KB

README.md

File metadata and controls

443 lines (372 loc) · 12.1 KB
Raw

850. 矩形面积 II

English Version

题目描述

我们给出了一个（轴对齐的）二维矩形列表 rectangles 。 对于 rectangle[i] = [xi1, yi1, xi2, yi2]，表示第 i 个矩形的坐标， (xi1, yi1) 是该矩形 左下角 的坐标， (xi2, yi2) 是该矩形 右上角 的坐标。

计算平面中所有 rectangles 所覆盖的 总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。

返回 总面积 。因为答案可能太大，返回 109 + 7 的 模 。

 

示例 1：

输入：rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出：6
解释：如图所示，三个矩形覆盖了总面积为6的区域。
从(1,1)到(2,2)，绿色矩形和红色矩形重叠。
从(1,0)到(2,3)，三个矩形都重叠。

示例 2：

输入：rectangles = [[0,0,1000000000,1000000000]]
输出：49
解释：答案是 1018 对 (109 + 7) 取模的结果， 即 49 。

 

提示：

  • 1 <= rectangles.length <= 200
  • rectanges[i].length = 4
  • 0 <= xi1, yi1, xi2, yi2 <= 109
  • 矩形叠加覆盖后的总面积不会超越 2^63 - 1 ，这意味着可以用一个 64 位有符号整数来保存面积结果。

解法

方法一：离散化 + 线段树 + 扫描线

线段树将整个区间分割为多个不连续的子区间，子区间的数量不超过 $log(width)$。更新某个元素的值，只需要更新 $log(width)$ 个区间，并且这些区间都包含在一个包含该元素的大区间内。区间修改时，需要使用懒标记保证效率。

  • 线段树的每个节点代表一个区间；
  • 线段树具有唯一的根节点，代表的区间是整个统计范围，如 $[1, N]$；
  • 线段树的每个叶子节点代表一个长度为 1 的元区间 $[x, x]$；
  • 对于每个内部节点 $[l, r]$，它的左儿子是 $[l, mid]$，右儿子是 $[mid + 1, r]$, 其中 $mid = ⌊(l + r) / 2⌋$ (即向下取整)。

对于本题，线段树节点维护的信息有：

  1. 区间被覆盖的次数 cnt；
  2. 区间被覆盖的长度 len。

另外，由于本题利用了扫描线本身的特性，因此，区间修改时，不需要懒标记，也无须进行 pushdown 操作。

Python3

class Node:
    def __init__(self):
        self.l = self.r = 0
        self.cnt = self.length = 0


class SegmentTree:
    def __init__(self, nums):
        n = len(nums) - 1
        self.nums = nums
        self.tr = [Node() for _ in range(n << 2)]
        self.build(1, 0, n - 1)

    def build(self, u, l, r):
        self.tr[u].l, self.tr[u].r = l, r
        if l != r:
            mid = (l + r) >> 1
            self.build(u << 1, l, mid)
            self.build(u << 1 | 1, mid + 1, r)

    def modify(self, u, l, r, k):
        if self.tr[u].l >= l and self.tr[u].r <= r:
            self.tr[u].cnt += k
        else:
            mid = (self.tr[u].l + self.tr[u].r) >> 1
            if l <= mid:
                self.modify(u << 1, l, r, k)
            if r > mid:
                self.modify(u << 1 | 1, l, r, k)
        self.pushup(u)

    def pushup(self, u):
        if self.tr[u].cnt:
            self.tr[u].length = self.nums[self.tr[u].r + 1] - \
                self.nums[self.tr[u].l]
        elif self.tr[u].l == self.tr[u].r:
            self.tr[u].length = 0
        else:
            self.tr[u].length = self.tr[u << 1].length + \
                self.tr[u << 1 | 1].length

    @property
    def length(self):
        return self.tr[1].length


class Solution:
    def rectangleArea(self, rectangles: List[List[int]]) -> int:
        segs = []
        alls = set()
        for x1, y1, x2, y2 in rectangles:
            segs.append((x1, y1, y2, 1))
            segs.append((x2, y1, y2, -1))
            alls.update([y1, y2])

        segs.sort()
        alls = sorted(alls)
        tree = SegmentTree(alls)
        m = {v: i for i, v in enumerate(alls)}
        ans = 0
        for i, (x, y1, y2, k) in enumerate(segs):
            if i:
                ans += tree.length * (x - segs[i - 1][0])
            tree.modify(1, m[y1], m[y2] - 1, k)
        ans %= int(1e9 + 7)
        return ans

Java

class Node {
    int l, r, cnt, length;
}

class SegmentTree {
    private Node[] tr;
    private int[] nums;

    public SegmentTree(int[] nums) {
        this.nums = nums;
        int n = nums.length - 1;
        tr = new Node[n << 2];
        for (int i = 0; i < tr.length; ++i) {
            tr[i] = new Node();
        }
        build(1, 0, n - 1);
    }

    private void build(int u, int l, int r) {
        tr[u].l = l;
        tr[u].r = r;
        if (l != r) {
            int mid = (l + r) >> 1;
            build(u << 1, l, mid);
            build(u << 1 | 1, mid + 1, r);
        }
    }

    public void modify(int u, int l, int r, int k) {
        if (tr[u].l >= l && tr[u].r <= r) {
            tr[u].cnt += k;
        } else {
            int mid = (tr[u].l + tr[u].r) >> 1;
            if (l <= mid) {
                modify(u << 1, l, r, k);
            }
            if (r > mid) {
                modify(u << 1 | 1, l, r, k);
            }
        }
        pushup(u);
    }

    private void pushup(int u) {
        if (tr[u].cnt > 0) {
            tr[u].length = nums[tr[u].r + 1] - nums[tr[u].l];
        } else if (tr[u].l == tr[u].r) {
            tr[u].length = 0;
        } else {
            tr[u].length = tr[u << 1].length + tr[u << 1 | 1].length;
        }
    }

    public int query() {
        return tr[1].length;
    }
}

class Solution {
    private static final int MOD = (int) 1e9 + 7;

    public int rectangleArea(int[][] rectangles) {
        int n = rectangles.length;
        int[][] segs = new int[n << 1][4];
        int i = 0;
        TreeSet<Integer> ts = new TreeSet<>();
        for (var e : rectangles) {
            int x1 = e[0], y1 = e[1], x2 = e[2], y2 = e[3];
            segs[i++] = new int[] {x1, y1, y2, 1};
            segs[i++] = new int[] {x2, y1, y2, -1};
            ts.add(y1);
            ts.add(y2);
        }
        Arrays.sort(segs, (a, b) -> a[0] - b[0]);
        Map<Integer, Integer> m = new HashMap<>(ts.size());
        i = 0;
        int[] nums = new int[ts.size()];
        for (int v : ts) {
            m.put(v, i);
            nums[i++] = v;
        }

        SegmentTree tree = new SegmentTree(nums);
        long ans = 0;
        for (i = 0; i < segs.length; ++i) {
            var e = segs[i];
            int x = e[0], y1 = e[1], y2 = e[2], k = e[3];
            if (i > 0) {
                ans += (long) tree.query() * (x - segs[i - 1][0]);
            }
            tree.modify(1, m.get(y1), m.get(y2) - 1, k);
        }
        ans %= MOD;
        return (int) ans;
    }
}

C++

class Node {
public:
    int l, r, cnt, length;
};

class SegmentTree {
public:
    vector<Node*> tr;
    vector<int> nums;

    SegmentTree(vector<int>& nums) {
        this->nums = nums;
        int n = nums.size() - 1;
        tr.resize(n << 2);
        for (int i = 0; i < tr.size(); ++i) tr[i] = new Node();
        build(1, 0, n - 1);
    }

    void build(int u, int l, int r) {
        tr[u]->l = l;
        tr[u]->r = r;
        if (l != r) {
            int mid = (l + r) >> 1;
            build(u << 1, l, mid);
            build(u << 1 | 1, mid + 1, r);
        }
    }

    void modify(int u, int l, int r, int k) {
        if (tr[u]->l >= l && tr[u]->r <= r)
            tr[u]->cnt += k;
        else {
            int mid = (tr[u]->l + tr[u]->r) >> 1;
            if (l <= mid) modify(u << 1, l, r, k);
            if (r > mid) modify(u << 1 | 1, l, r, k);
        }
        pushup(u);
    }

    int query() {
        return tr[1]->length;
    }

    void pushup(int u) {
        if (tr[u]->cnt)
            tr[u]->length = nums[tr[u]->r + 1] - nums[tr[u]->l];
        else if (tr[u]->l == tr[u]->r)
            tr[u]->length = 0;
        else
            tr[u]->length = tr[u << 1]->length + tr[u << 1 | 1]->length;
    }
};

class Solution {
public:
    const int mod = 1e9 + 7;

    int rectangleArea(vector<vector<int>>& rectangles) {
        int n = rectangles.size();
        vector<vector<int>> segs(n << 1);
        set<int> ts;
        int i = 0;
        for (auto& e : rectangles) {
            int x1 = e[0], y1 = e[1], x2 = e[2], y2 = e[3];
            segs[i++] = {x1, y1, y2, 1};
            segs[i++] = {x2, y1, y2, -1};
            ts.insert(y1);
            ts.insert(y2);
        }
        sort(segs.begin(), segs.end());
        unordered_map<int, int> m;
        i = 0;
        for (int v : ts) m[v] = i++;
        vector<int> nums(ts.begin(), ts.end());
        SegmentTree* tree = new SegmentTree(nums);
        long long ans = 0;
        for (int i = 0; i < segs.size(); ++i) {
            auto e = segs[i];
            int x = e[0], y1 = e[1], y2 = e[2], k = e[3];
            if (i > 0) ans += (long long) tree->query() * (x - segs[i - 1][0]);
            tree->modify(1, m[y1], m[y2] - 1, k);
        }
        ans %= mod;
        return (int) ans;
    }
};

Go

func rectangleArea(rectangles [][]int) int {
	var mod int = 1e9 + 7
	segs := [][]int{}
	alls := map[int]bool{}
	for _, e := range rectangles {
		x1, y1, x2, y2 := e[0], e[1], e[2], e[3]
		segs = append(segs, []int{x1, y1, y2, 1})
		segs = append(segs, []int{x2, y1, y2, -1})
		alls[y1] = true
		alls[y2] = true
	}
	nums := []int{}
	for v := range alls {
		nums = append(nums, v)
	}
	sort.Ints(nums)
	sort.Slice(segs, func(i, j int) bool { return segs[i][0] < segs[j][0] })
	m := map[int]int{}
	for i, v := range nums {
		m[v] = i
	}
	tree := newSegmentTree(nums)
	ans := 0
	for i, e := range segs {
		x, y1, y2, k := e[0], e[1], e[2], e[3]
		if i > 0 {
			ans += tree.query() * (x - segs[i-1][0])
			ans %= mod
		}
		tree.modify(1, m[y1], m[y2]-1, k)
	}
	return ans
}

type node struct {
	l      int
	r      int
	cnt    int
	length int
}

type segmentTree struct {
	tr   []*node
	nums []int
}

func newSegmentTree(nums []int) *segmentTree {
	n := len(nums) - 1
	tr := make([]*node, n<<2)
	for i := range tr {
		tr[i] = &node{}
	}
	t := &segmentTree{tr, nums}
	t.build(1, 0, n-1)
	return t
}

func (t *segmentTree) build(u, l, r int) {
	t.tr[u].l, t.tr[u].r = l, r
	if l == r {
		return
	}
	mid := (l + r) >> 1
	t.build(u<<1, l, mid)
	t.build(u<<1|1, mid+1, r)
}

func (t *segmentTree) modify(u, l, r, k int) {
	if t.tr[u].l >= l && t.tr[u].r <= r {
		t.tr[u].cnt += k
	} else {
		mid := (t.tr[u].l + t.tr[u].r) >> 1
		if l <= mid {
			t.modify(u<<1, l, r, k)
		}
		if r > mid {
			t.modify(u<<1|1, l, r, k)
		}
	}
	t.pushup(u)
}

func (t *segmentTree) query() int {
	return t.tr[1].length
}

func (t *segmentTree) pushup(u int) {
	if t.tr[u].cnt > 0 {
		t.tr[u].length = t.nums[t.tr[u].r+1] - t.nums[t.tr[u].l]
	} else if t.tr[u].l == t.tr[u].r {
		t.tr[u].length = 0
	} else {
		t.tr[u].length = t.tr[u<<1].length + t.tr[u<<1|1].length
	}
}

...