|
1 | | -# RNN(循环神经网络) |
| 1 | +# RNN(循环神经网络) |
| 2 | + |
| 3 | +- RNN对具有**序列特性**的数据非常有效,它能挖掘数据中的**时序信息以及语义信息** |
| 4 | + |
| 5 | +- RNN的这种能力,使深度学习模型在解决**语音识别、语言模型、机器翻译以及时序分析**等NLP领域的问题时有所突破 |
| 6 | + |
| 7 | +举个例子: |
| 8 | + |
| 9 | +I saw a saw. |
| 10 | + |
| 11 | +如果我们想对这个句子的单词标注词性,那么saw一个作为动词,一个作为名词,他的输入是一模一样的,相互之间没有区别,那么得到的结果也会一样。 |
| 12 | + |
| 13 | +但是如果考虑序列的影响,一个位置在前面,一个位置在后面,我们自然而然地会认为前者是动词,后者是名词。 |
| 14 | + |
| 15 | + |
| 16 | + |
| 17 | + |
| 18 | + |
| 19 | +如果没有带箭头的圆,那么他就是一个全连接层。现在有了一个圆转了一圈,就说明我们隐藏层上产生的结果也会影响自身。 |
| 20 | + |
| 21 | +U是输入层到隐藏层的**权重矩阵**,o也是一个向量,它表示**输出层**的值;V是隐藏层到输出层的**权重矩阵**。 |
| 22 | + |
| 23 | +> W是什么捏? |
| 24 | +
|
| 25 | +循环神经网络**的**隐藏层**的值s不仅仅取决于当前这次的输入x,还取决于上一次**隐藏层**的值s**。**权重矩阵W**就是**隐藏层**上一次的值作为这一次的输入的权重。 |
| 26 | + |
| 27 | +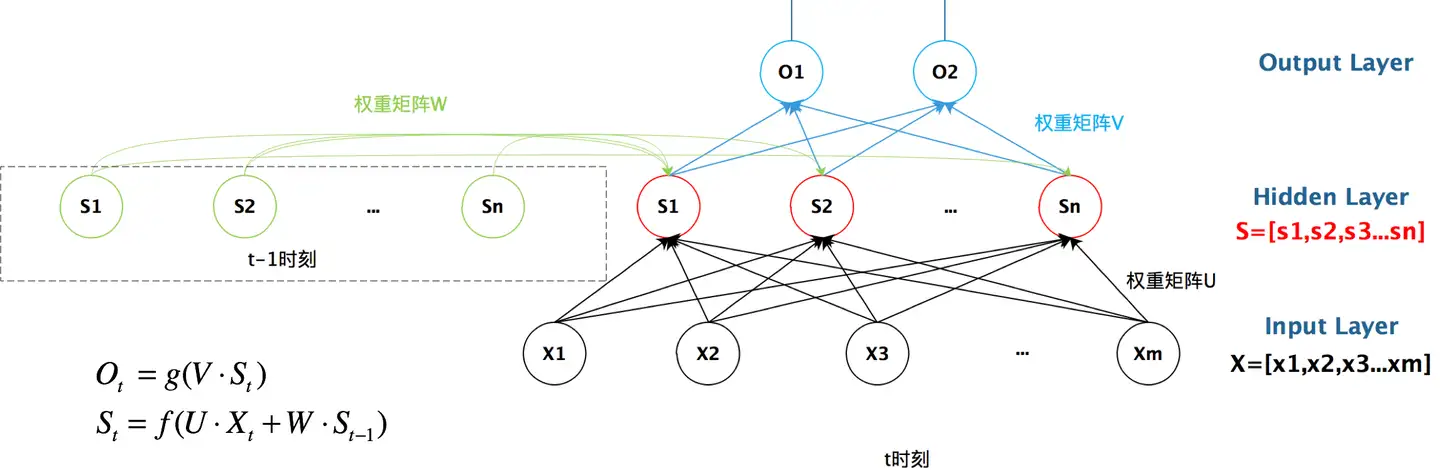 |
| 28 | + |
| 29 | + |
| 30 | + |
| 31 | +- 上一时刻的隐藏层是如何影响当前时刻的隐藏层的 |
| 32 | + |
| 33 | +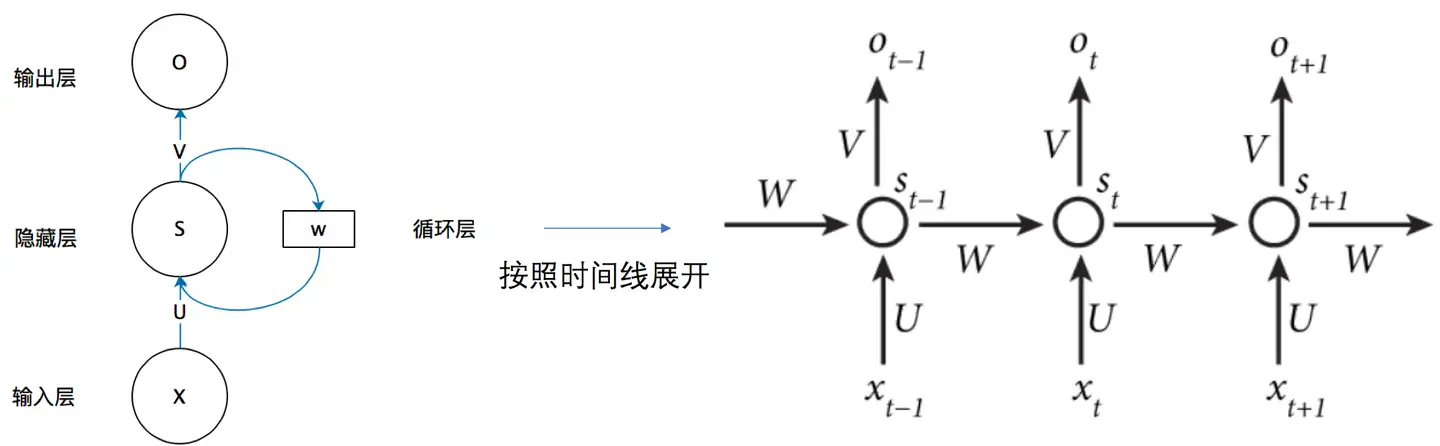 |
| 34 | + |
| 35 | +**优点**: |
| 36 | + |
| 37 | +- 能够处理不同长度的序列数据。 |
| 38 | +- 能够捕捉序列中的时间依赖关系。 |
| 39 | + |
| 40 | +**缺点**: |
| 41 | + |
| 42 | +- 对长序列的记忆能力较弱,可能出现梯度消失或梯度爆炸问题。(梯度特别大或者特别小) |
| 43 | +- 训练可能相对复杂和时间消耗大。 |
| 44 | + |
| 45 | +> 下面是两个RNN的高级版,我们所说的使用RNN也一般是使用LSTM和GRU。 |
| 46 | +
|
| 47 | +# LSTM(长短时记忆网络) |
| 48 | + |
| 49 | +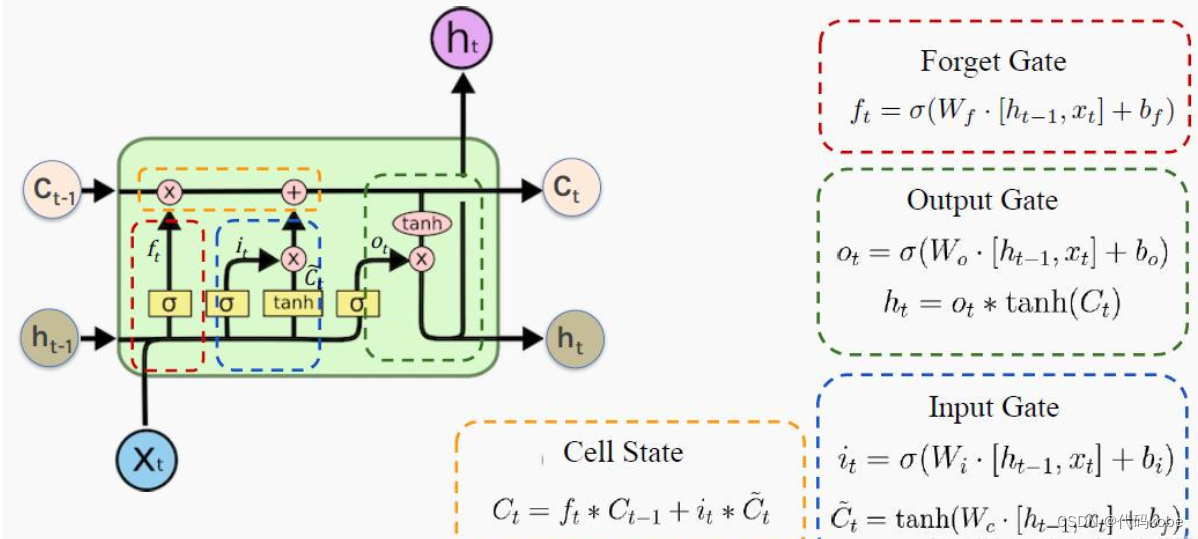 |
| 50 | + |
| 51 | +遗忘门:通过x和ht的操作,并经过sigmoid函数,得到0,1的向量,0对应的就代表之前的记忆某一部分要忘记,1对应的就代表之前的记忆需要留下的部分。 |
| 52 | + |
| 53 | +> 代表复习上一门线性代数所包含的记忆,通过遗忘门,忘记掉和下一门高等数学无关的内容(比如矩阵的秩) |
| 54 | +
|
| 55 | +输入门:通过将之前的需要留下的信息和现在需要记住的信息相加,也就是得到了新的记忆状态。 |
| 56 | + |
| 57 | +> 代表复习下一门科目高等数学的时候输入的一些记忆(比如洛必达法则等等),那么已经线性代数残余且和高数相关的部分(比如数学运算)+高数的知识=新的记忆状态 |
| 58 | +
|
| 59 | +输出门:整合,得到一个输出。 |
| 60 | + |
| 61 | +> 代表高数所需要的记忆,但是在实际的考试不一定全都发挥出来考到100分。因此,则代表实际的考试分数 |
| 62 | +
|
| 63 | +遗忘门 |
| 64 | + |
| 65 | +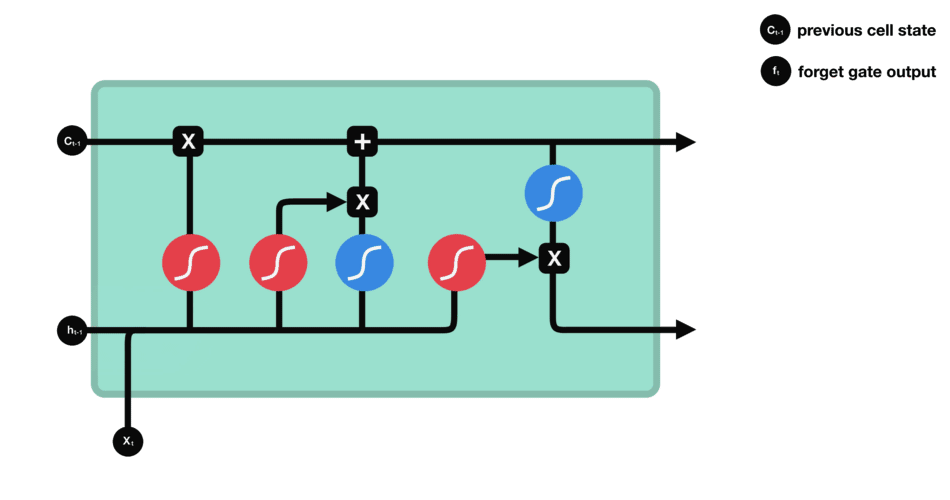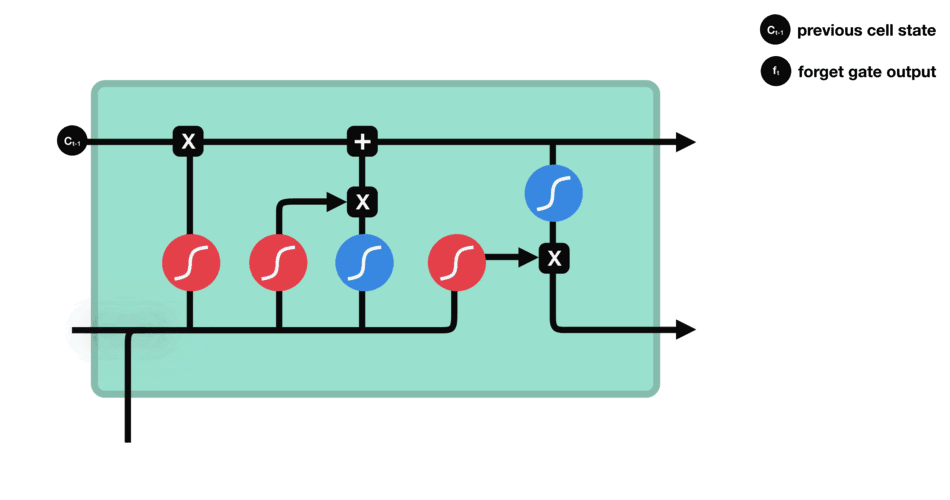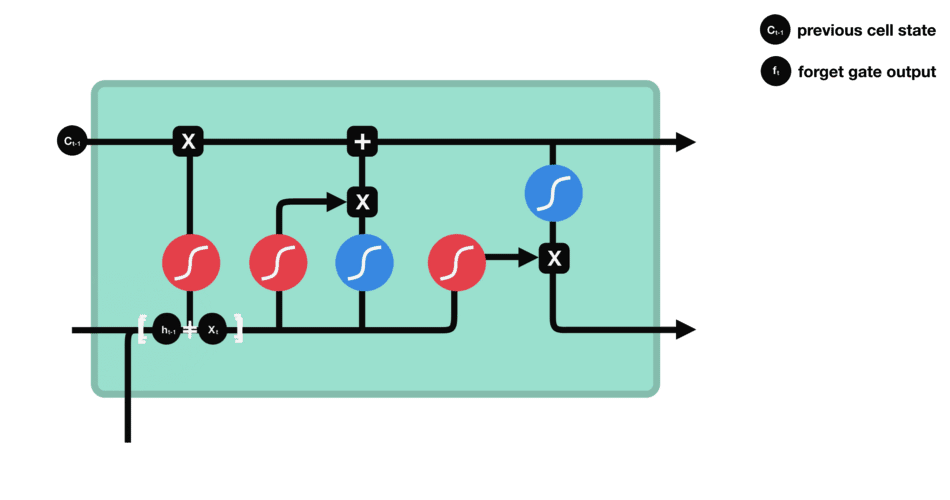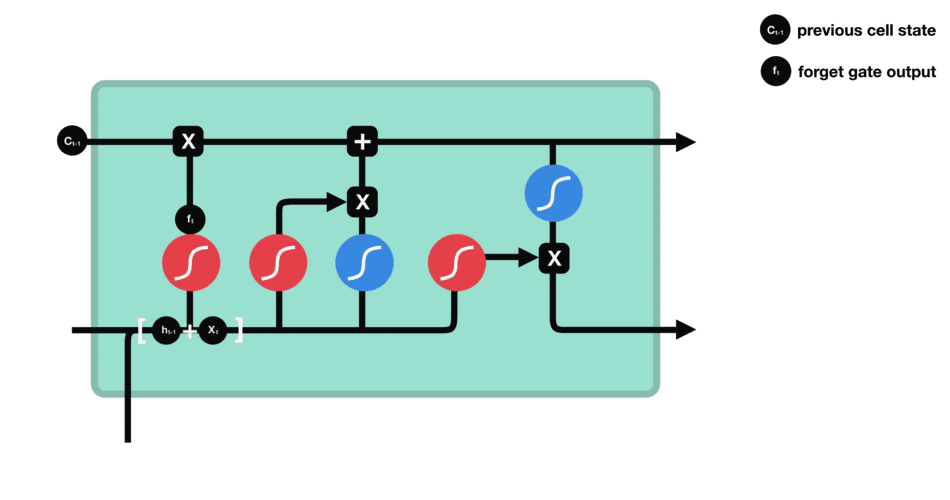 |
| 66 | + |
| 67 | +输入门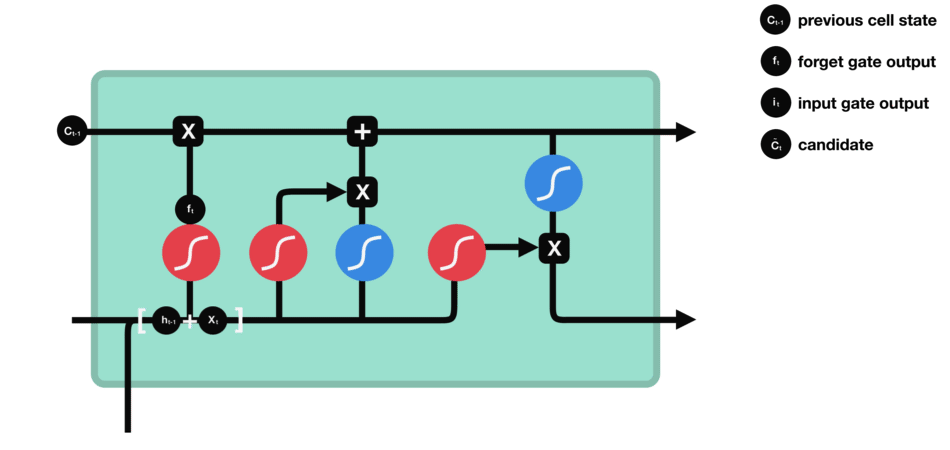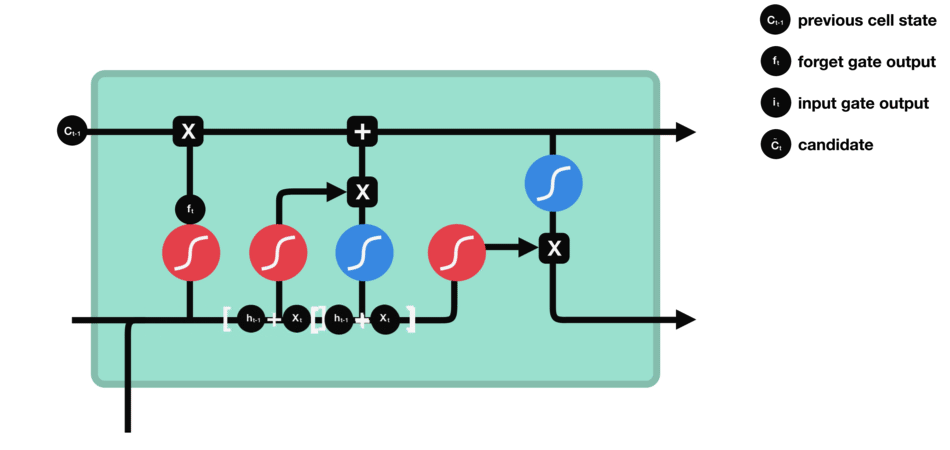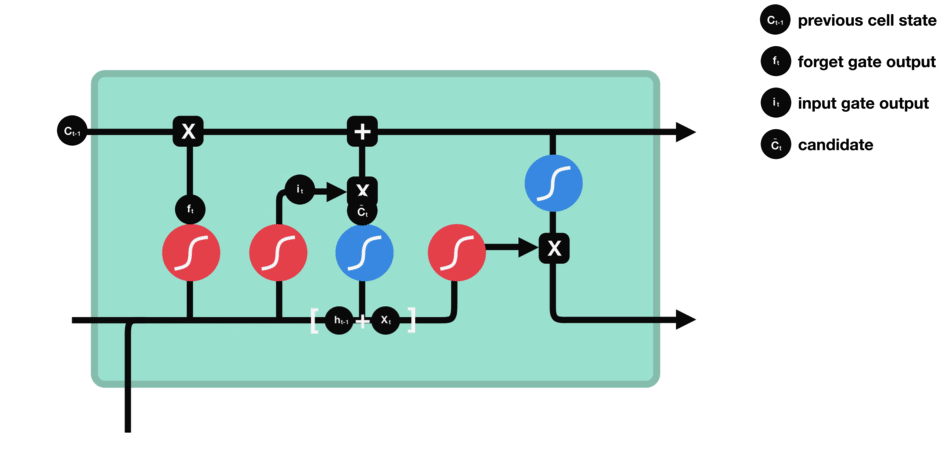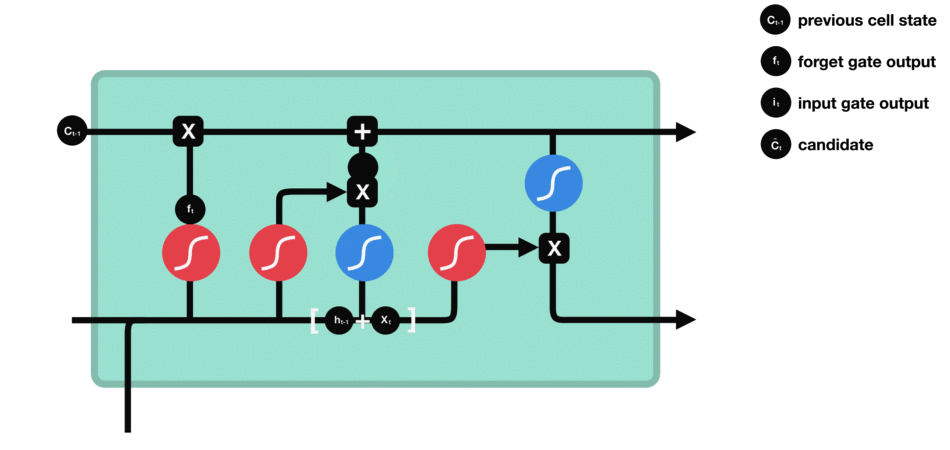 |
| 68 | + |
| 69 | +细胞状态 |
| 70 | + |
| 71 | + |
| 72 | + |
| 73 | +输出门 |
| 74 | + |
| 75 | +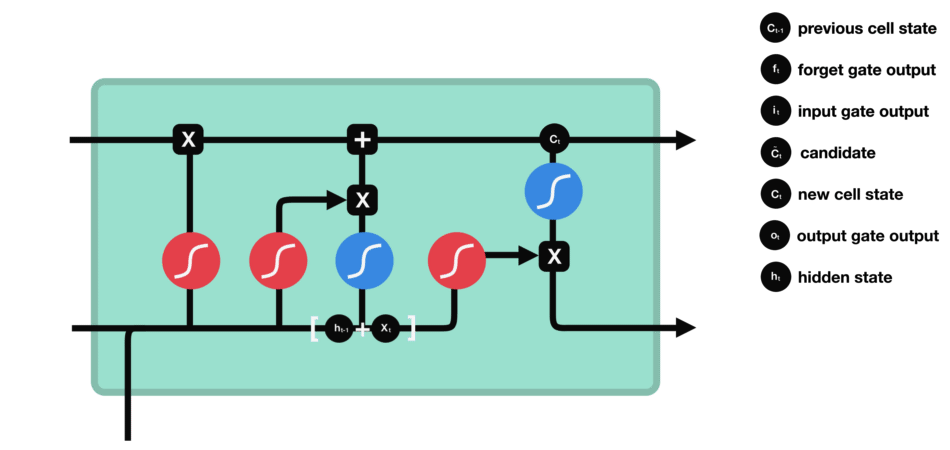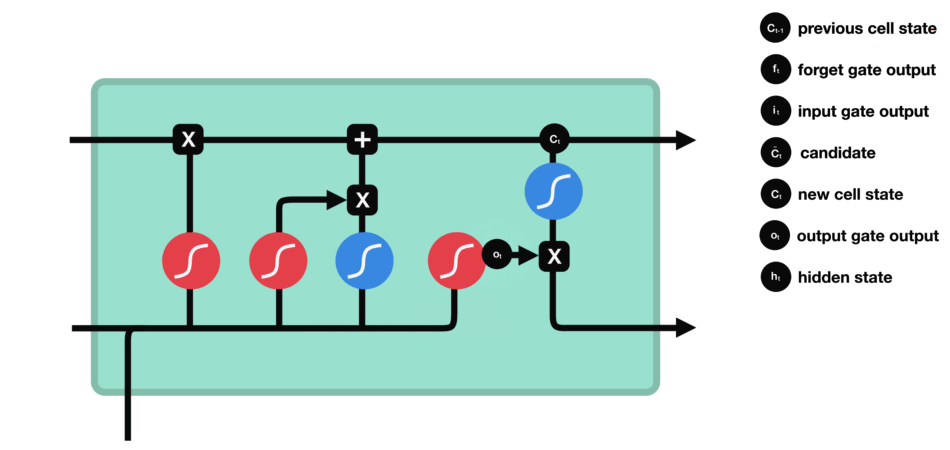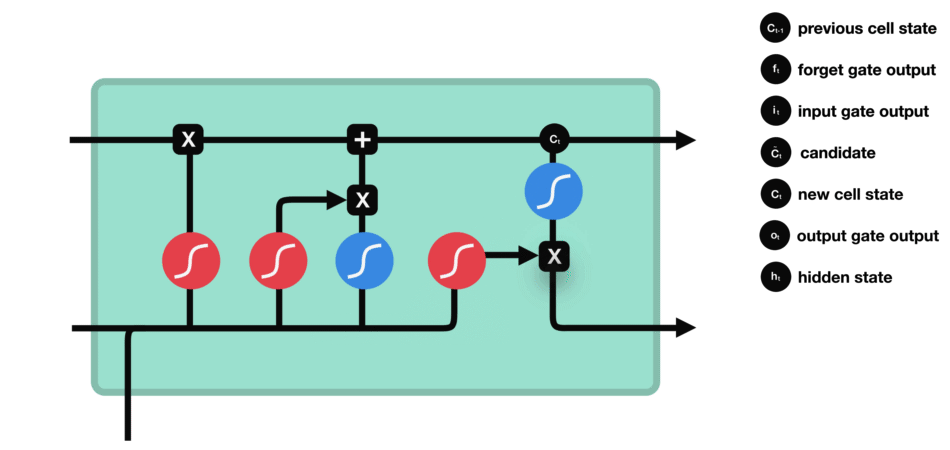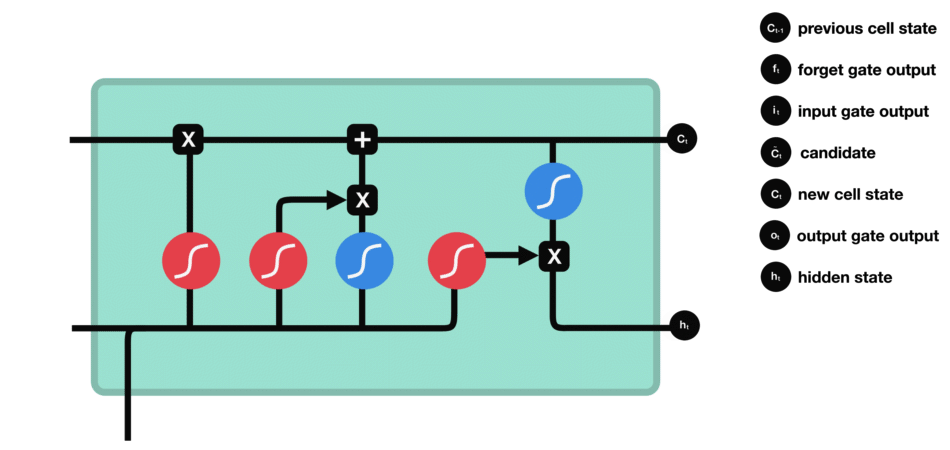 |
| 76 | + |
| 77 | +LSTM通过引入复杂的门控机制解决了梯度消失的问题,使其能够捕获更长的序列依赖关系。然而,LSTM的复杂结构也使其在计算和参数方面相对昂贵。 |
| 78 | + |
| 79 | +```python |
| 80 | +# LSTM的PyTorch实现 |
| 81 | +import torch.nn as nn |
| 82 | + |
| 83 | +class LSTM(nn.Module): |
| 84 | + def __init__(self, input_size, hidden_size, output_size): |
| 85 | + super(LSTM, self).__init__() |
| 86 | + self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True) |
| 87 | + # input_size: 输入数据的特征维度大小。 |
| 88 | + # 在时间序列中,它通常对应于每个时间步的特征数量 |
| 89 | + # hidden_size: LSTM单元的隐藏状态的维度大小。它表示网络内部学习的表示空间的大小 |
| 90 | + # batch_first: 指定输入数据的维度顺序。当设置为True时,输入数据的维度顺序为 (batch_size, sequence_length, input_size)。这通常在处理批次数据时更方便。 |
| 91 | + self.fc = nn.Linear(hidden_size, output_size) |
| 92 | + |
| 93 | + def forward(self, x, (h_0, c_0)): |
| 94 | + out, (h_n, c_n) = self.lstm(x, (h_0, c_0)) # 运用LSTM层 |
| 95 | + # (h_0, c_0): LSTM的初始隐藏状态和细胞状态 |
| 96 | + # (h_n, c_n): LSTM的最终隐藏状态和细胞状态 |
| 97 | + out = self.fc(out) # 运用全连接层 |
| 98 | + return out |
| 99 | +``` |
| 100 | + |
| 101 | +# GRU(门控循环单元) |
| 102 | + |
| 103 | +r是控制重置的门空、z为控制更新的门控 |
| 104 | +$$ |
| 105 | +\sigma 是sigmoid函数,通过这个函数可以使数据变换为0-1范围内的数值,从而来充当门控信号。 |
| 106 | +$$ |
| 107 | +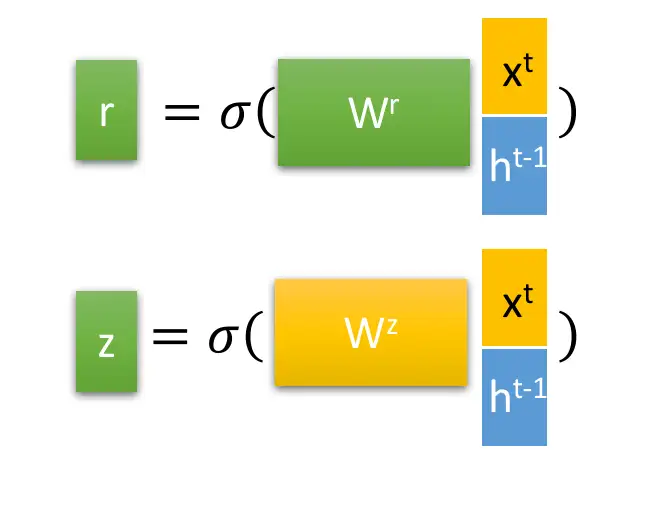 |
| 108 | + |
| 109 | +$得到门控信号之后,首先使用重置门控来得到“重置”之后的数据 {h^{t-1}}' = h^{t-1} \odot r,$ |
| 110 | + |
| 111 | +$再将 {h^{t-1}}' 与输入 x^t 进行拼接,再通过一个tanh激活函数来将数据放缩到[-1,1]的范围内。$ |
| 112 | + |
| 113 | +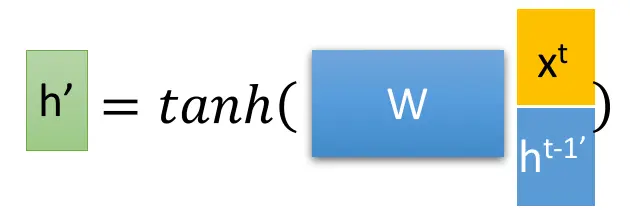 |
| 114 | + |
| 115 | +$\odot 是Hadamard Product,也就是操作矩阵中对应的元素相乘,因此要求两个相乘矩阵是同型的。\oplus 则代表进行矩阵加法操作。$ |
| 116 | + |
| 117 | +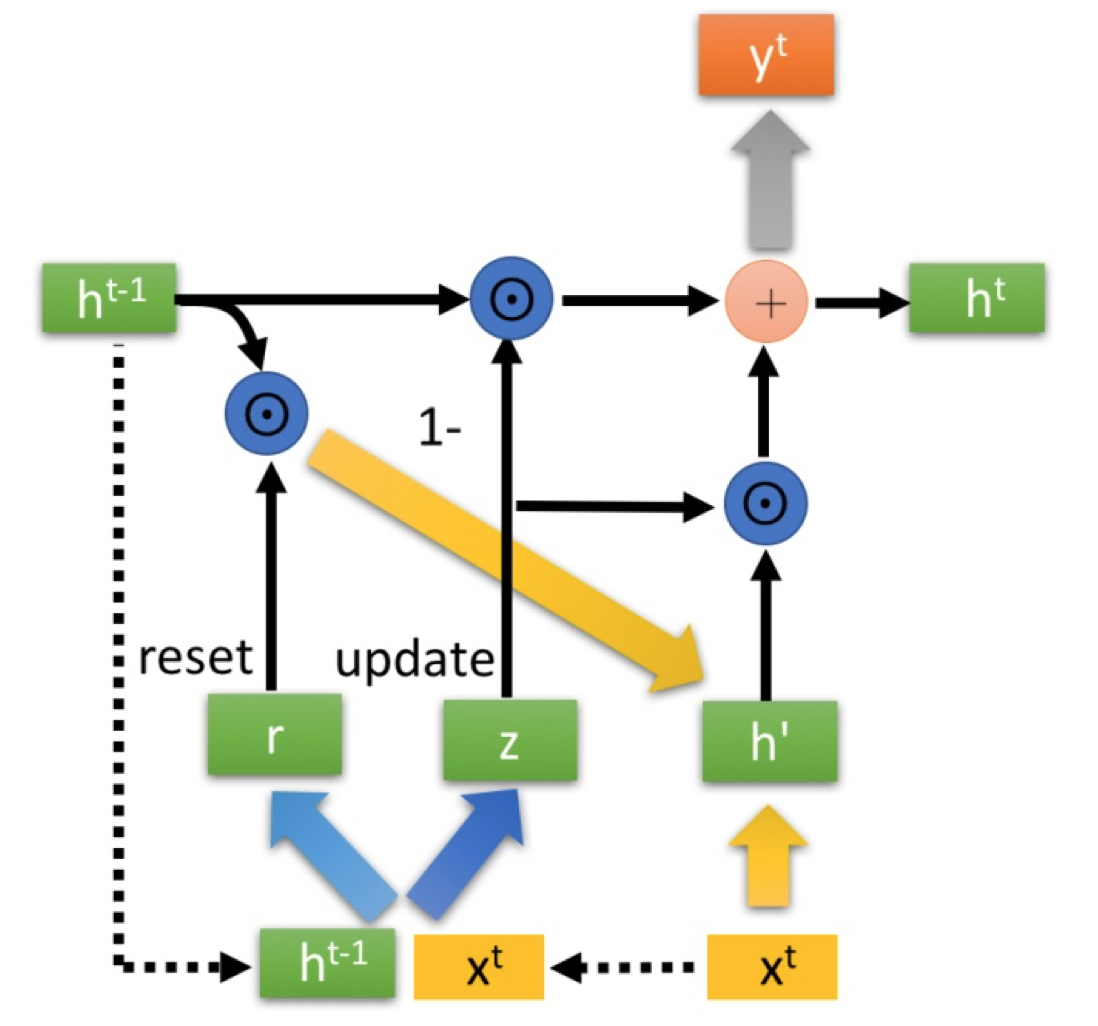 |
| 118 | +$$ |
| 119 | +更新表达式: h^t = (1-z) \odot h^{t-1} + z\odot h' |
| 120 | +$$ |
| 121 | +再次强调一下,门控信号(这里的 z )的范围为0~1。门控信号越接近1,代表”记忆“下来的数据越多;而越接近0则代表”遗忘“的越多。 |
| 122 | + |
| 123 | +GRU很聪明的一点就在于,**我们使用了同一个门控 z 就同时可以进行遗忘和选择记忆(LSTM则要使用多个门控** |
| 124 | + |
| 125 | +- $(1-z) \odot h^{t-1} :表示对原本隐藏状态的选择性“遗忘”。$ |
| 126 | + |
| 127 | + $这里的 1-z 可以想象成遗忘门(forget \quad gate),忘记 h^{t-1} 维度中一些不重要的信息。$ |
| 128 | + |
| 129 | +- $z \odot h' : 表示对包含当前节点信息的 h' 进行选择性记忆。$$与上面类似,这里的 (1-z) 同理会忘记 h ' 维度中的一些不重要的信息。$$或者,这里我们更应当看做是对 h' 维度中的某些信息进行选择。$ |
| 130 | + |
| 131 | +- $h^t =(1- z) \odot h^{t-1} + z\odot h' $$结合上述,这一步的操作就是忘记传递下来的 h^{t-1} 中的某些维度信息,并加入当前节点输入的某些维度信息。$ |
| 132 | + |
| 133 | +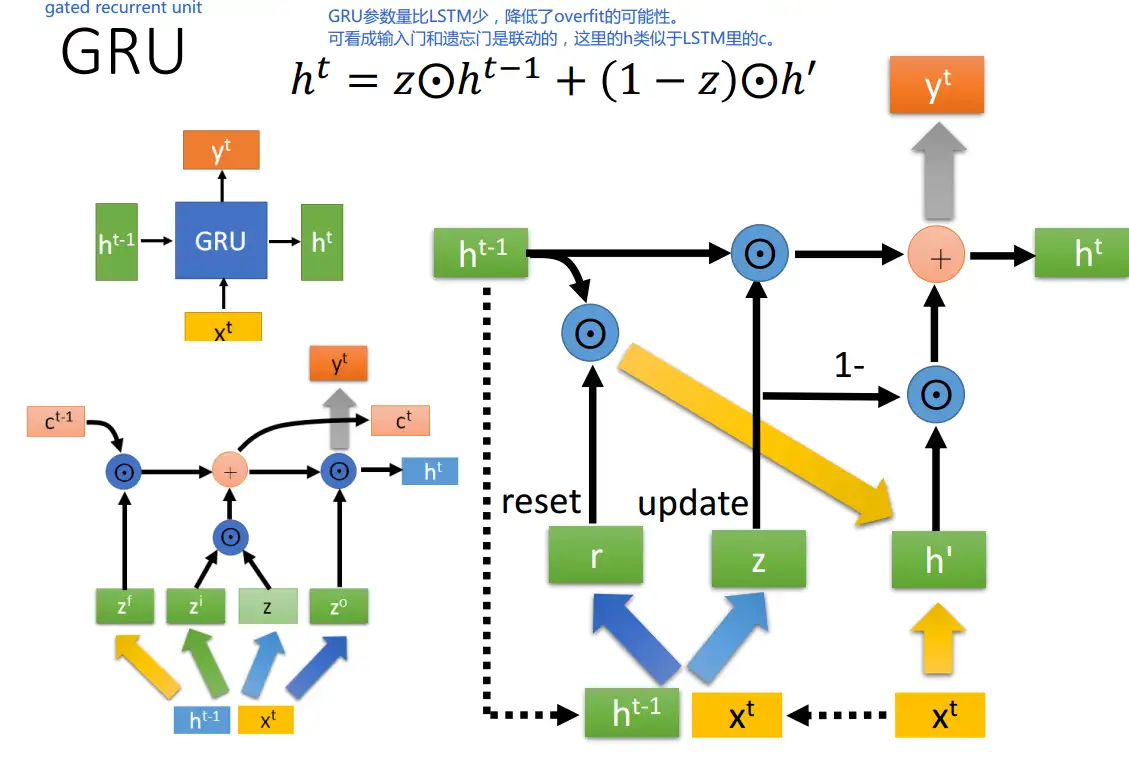 |
| 134 | + |
| 135 | +```python |
| 136 | +# GRU的PyTorch实现 |
| 137 | +import torch.nn as nn |
| 138 | + |
| 139 | +class GRU(nn.Module): |
| 140 | + def __init__(self, input_size, hidden_size, output_size): |
| 141 | + super(GRU, self).__init__() |
| 142 | + self.gru = nn.GRU(input_size, hidden_size, batch_first=True) |
| 143 | + self.fc = nn.Linear(hidden_size, output_size) |
| 144 | + |
| 145 | + def forward(self, x, h_0): |
| 146 | + out, h_n = self.gru(x, h_0) # 运用GRU层 |
| 147 | + out = self.fc(out) # 运用全连接层 |
| 148 | + return out |
| 149 | +``` |
| 150 | + |
| 151 | +# 区别 |
| 152 | + |
| 153 | +GRU和LSTM的主要区别: |
| 154 | + |
| 155 | +1. **细胞状态的管理:** LSTM通过细胞状态来管理长期记忆,而GRU直接使用隐藏状态来传递信息。 |
| 156 | +2. **门控机制数量:** LSTM有输入门、遗忘门和输出门,而GRU只有更新门和重置门,减少了门控机制的数量。 |
| 157 | +3. **参数数量:** 通常情况下,GRU的参数数量较少,因此在一些情境下可能更容易训练。 |
| 158 | + |
| 159 | +# Bi-RNN(双向循环神经网络) |
| 160 | + |
| 161 | +双向循环神经网络(Bidirectional Recurrent Neural Network,Bi-RNN)是一种能够捕获序列数据前后依赖关系的RNN架构。通过结合正向和反向的信息流,Bi-RNN可以更全面地理解序列中的模式。 |
| 162 | + |
| 163 | +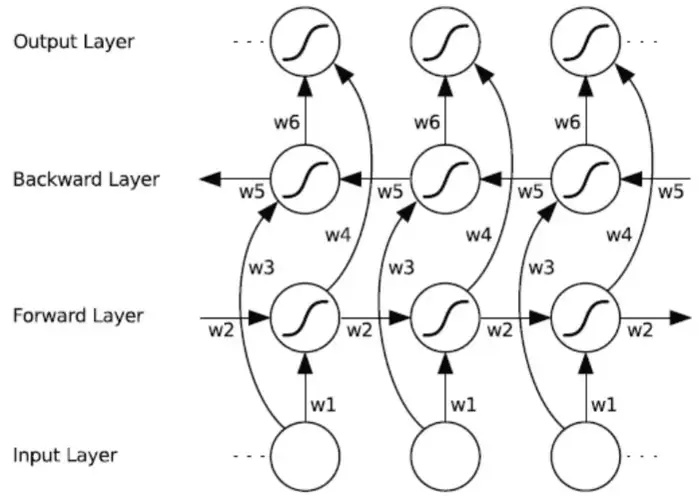 |
| 164 | + |
| 165 | +Bi-RNN由两个独立的RNN层组成,一个正向层和一个反向层。这两个层分别处理输入序列的正向和反向版本。 |
| 166 | + |
| 167 | +正向和反向层的隐藏状态通常通过连接或其他合并方式结合在一起,以形成最终的隐藏状态 |
| 168 | + |
| 169 | +```python |
| 170 | +# Bi-RNN的PyTorch实现 |
| 171 | +import torch.nn as nn |
| 172 | + |
| 173 | +class BiRNN(nn.Module): |
| 174 | + def __init__(self, input_size, hidden_size, output_size): |
| 175 | + super(BiRNN, self).__init__() |
| 176 | + self.rnn = nn.RNN(input_size, hidden_size, batch_first=True, bidirectional=True) |
| 177 | + self.fc = nn.Linear(hidden_size * 2, output_size) |
| 178 | + |
| 179 | + def forward(self, x): |
| 180 | + out, _ = self.rnn(x) # 运用双向RNN层 |
| 181 | + out = self.fc(out) # 运用全连接层 |
| 182 | + return out |
| 183 | +``` |
| 184 | + |
| 185 | +> Bi-RNN可以与其他RNN结构(例如LSTM和GRU)相结合,进一步增强其能力。 |
| 186 | +
|
| 187 | +# word embedding(词嵌入) |
| 188 | + |
| 189 | +再来介绍一个自然语言处理中的概念——词嵌入(word embedding),也可以称为词向量。 |
| 190 | + |
| 191 | +图像分类问题会使用one-hot编码,比如一共有5个类,那么第二类的编码就是 (0, 1, 0, 0, 0),对于分类问题,这样当然特别简明。但是在自然语言处理中,因为单词的数目过多,这样做会导致输入维度过高,而且无法让机器理解语义。 |
| 192 | + |
| 193 | +换句话说,我们更希望能掌握不同单词之间的相似程度。 |
| 194 | + |
| 195 | +> 为什么使用词嵌入? |
| 196 | +
|
| 197 | +使用词嵌入模型可以让模型更好的理解词与词之间的类比,比如:男人和女人,国王和王后。 |
| 198 | + |
| 199 | +- **特征表征(Featurized representation):**对每个单词进行编码。也就是使用一个特征向量表征单词,特征向量的每个元素都是对该单词某一特征的量化描述,量化范围可以是**[-1,1]**之间。特征表征的例子如下: |
| 200 | + |
| 201 | + 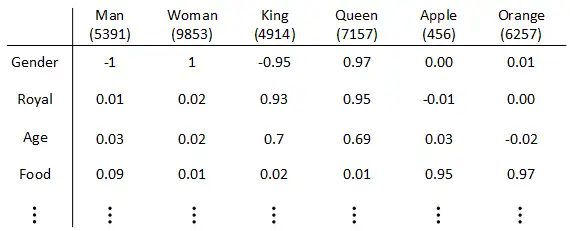 |
| 202 | + |
| 203 | +- 特征向量的长度依情况而定,**特征元素越多则对单词表征得越全面**。这里的特征向量长度设定为300。使用特征表征之后,词汇表中的每个单词都可以使用对应的300 x 1的向量来表示,该**向量的每个元素表示该单词对应的某个特征值**。每个单词用e+词汇表索引的方式标记,例如:**e5391,e9853,e4914** |
| 204 | +- 这种特征表征的优点是**根据特征向量能清晰知道不同单词之间的相似程度**,例如Apple和Orange之间的相似度较高,很可能属于同一类别。这种单词“类别”化的方式,大大提高了有限词汇量的泛化能力,这种特征化单词的操作被称为**Word Embeddings**,即**词嵌入** |
| 205 | +- 值得一提的是,这里特征向量的每个特征元素含义是具体的,对应到实际特征,例如性别、年龄等。而在实际应用中,特征向量**很多特征元素并不一定对应到有物理意义的特征**,是比较抽象的。但是,这并不影响对每个单词的有效表征,同样能比较不同单词之间的相似性。**每个单词都由高维特征向量表征,为了可视化不同单词之间的相似性,可以使用降维操作**,例如t-SNE算法,将300D降到2D平面上。如下图所示: |
| 206 | + |
| 207 | + |
| 208 | + |
| 209 | +从上图可以看出相似的单词分布距离较近,从而也证明了Word Embeddings能有效表征单词的关键特征。 |
| 210 | + |
| 211 | +**词嵌入的特性** |
| 212 | + |
| 213 | +常识地,“Man”与“Woman”的关系类比于“King”与“Queen”的关系 |
| 214 | + |
| 215 | +- 将“Man”的embedding vector与“Woman”的embedding vector相减: |
| 216 | + |
| 217 | +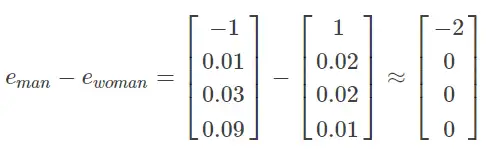 |
| 218 | + |
| 219 | +- 将“King”的embedding vector与“Queen”的embedding vector相减: |
| 220 | + |
| 221 | +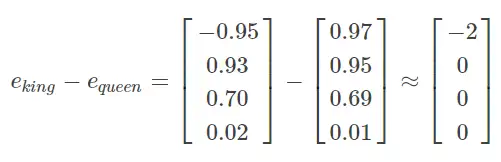 |
| 222 | + |
| 223 | +- 相减结果表明,“Man”与“Woman”的主要区别是性别,“King”与“Queen”也是一样。一般地,A类比于B相当于C类比于“?”,这类问题可以使用embedding vector进行运算。 |
| 224 | + |
| 225 | +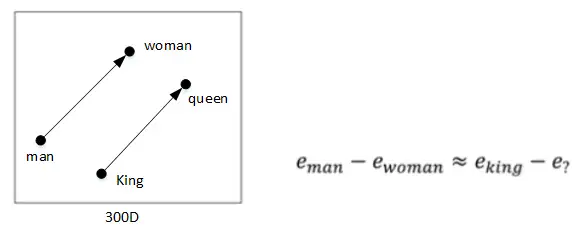 |
| 226 | + |
| 227 | +- 如上图所示,根据等式$e_{man}−e_{woman}≈e_{king}−e_?$得: |
| 228 | + |
| 229 | + $e_?=e_{king}−e_{man}+e_{woman}$利用相似函数 |
| 230 | + |
| 231 | + 计算与$e_{king}−e_{man}+e_{woman}$相似性最大的$e_?$ |
| 232 | + |
| 233 | + 得到$e_?=e_{queen}$ |
| 234 | + |
| 235 | +- 关于**相似函数**,比较常用的是**cosine similarity,**其表达式为:$Sim(u,v)=(u^T)⋅v/(||u||⋅||v||)$ |
| 236 | + |
| 237 | +- 还可以计算Euclidian distance来比较相似性,即$||u−v||^2$。距离越大,相似性越小 |
| 238 | + |
0 commit comments